Advertisements
Advertisements
प्रश्न
Using Bohr’s postulates, obtain the expression for the total energy of the electron in the stationary states of the hydrogen atom. Hence draw the energy level diagram showing how the line spectra corresponding to Balmer series occur due to transition between energy levels.
उत्तर
According to Bohr’s postulates, in a hydrogen atom, a single alectron revolves around a nucleus of charge +e. For an electron moving with a uniform speed in a circular orbit os a given radius, the centripetal force is provided by Columb force of attraction between the electron and the nucleus. The gravitational attraction may be neglected as the mass of electron and proton is very small.
So,
`(mv^2)/r = (ke^2)/r^2`
or `mv^2 = (ke^2)/r .............. (1)`
where m = mass of electron
r = radius of electronic orbit
v = velocity of electron.
Again,
`mvr = (nh)/(2π)`
or `v = (nh)/(2πmr)`
From eq.(1), we get,
`m((nh)/(2πmr)^2) = (ke^2)/r`
`=> r = (n^2h^2)/(4π^2kme^2).....................(2)`
(i) Kinetic energy of electron,
`E_k = 1/2 mv^2 = (ke^2)/(2r)`
Using eq (2), we get
`Ek =ke^2/2 (4π^2kme^2)/(n^2h^2)`
=`(4π^2kme^2)/(n^2h^2)`
`(2π^2k^2me^4)/(n^2h^2)`
(ii) Potential energy
`E_p = -(k(e) xx (e))/r = - (ke^2) / r `
Using eq (2), we get
`E^p =-ke^2 xx (4π^2kme^2)/(n^2h^2)`
= `-(4π^2k^2me^4)/(n^2h^2)`
Hence, total energy of the electron in the nth orbit
`E =E_p+E_k =(4π^2k^2me^4)/(n^2h^2)+(2π^2k^2me^4)/(n^2h^2) =- (2π^2k^2me^4)/(n^2h^2) =- (13.6)/n^2 eV `
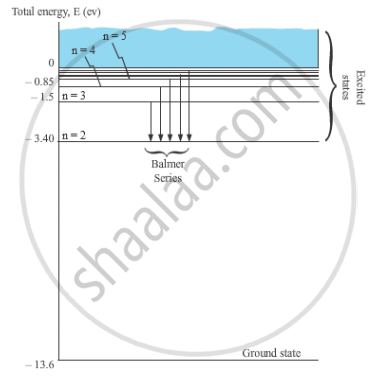
When the electron in a hydrogen atom jumps from higher energy level to the lower energy level, the difference of energies of the two energy levels is emitted as a radiation of particular wavelength. It is called a spectral line.
In H-atom, when an electron jumps from the orbit ni to orbit nf, the wavelength of the emitted radiation is given by,
`1/λ = R (1/n_f^2 -1/n_i^2)`
Where,
R → Rydberg’s constant = 1.09678 ×107 m−1
For Balmer series, nf = 2 and ni = 3, 4, 5, …
`1/λ = R (1/2^2 -1/n_i^2)`
Where, ni = 3, 4, 5, …
These spectral lines lie in the visible region.
APPEARS IN
संबंधित प्रश्न
An electron is orbiting in 5th Bohr orbit. Calculate ionisation energy for this atom, if the ground state energy is -13.6 eV.
The longest wavelength doublet absorption transition is observed at 589 and 589.6 nm. Calculate the frequency of each transition and energy difference between two excited states.
The ratio of kinetic energy of an electron in Bohr’s orbit to its total energy in the same orbit is
(A) – 1
(B) 2
(C) 1/2
(D) – 0.5
Balmer series was observed and analysed before the other series. Can you suggest a reason for such an order?
A beam of light having wavelengths distributed uniformly between 450 nm to 550 nm passes through a sample of hydrogen gas. Which wavelength will have the least intensity in the transmitted beam?
A parallel beam of light of wavelength 100 nm passes through a sample of atomic hydrogen gas in ground state. (a) Assume that when a photon supplies some of its energy to a hydrogen atom, the rest of the energy appears as another photon. Neglecting the light emitted by the excited hydrogen atoms in the direction of the incident beam, what wavelengths may be observed in the transmitted beam? (b) A radiation detector is placed near the gas to detect radiation coming perpendicular to the incident beam. Find the wavelengths of radiation that may be detected by the detector.
Consider two different hydrogen atoms. The electron in each atom is in an excited state. Is it possible for the electrons to have different energies but same orbital angular momentum according to the Bohr model? Justify your answer.
The energy required to remove the electron from a singly ionized Helium atom is 2.2 times the energy required to remove an electron from Helium atom. The total energy required to ionize the Helium atom completely is ______.
What is meant by ionisation energy?
Specify the transition of an electron in the wavelength of the line in the Bohr model of the hydrogen atom which gives rise to the spectral line of the highest wavelength ______.
