Advertisements
Advertisements
Question
Using the Remainder and Factor Theorem, factorise the following polynomial:
`x^3 + 10x^2 - 37x + 26`
Solution
`f(x) = x^3 + 10x^2 - 37x + 26`
For x = 1
`f(1) = (1)^2 + 10(1)^2 - 37(1) + 26`
= 1 + 10 - 37 + 26
= 0
=> (x - 1) is a factor of `x^3 + 10x^2 - 37x + 26`
Now
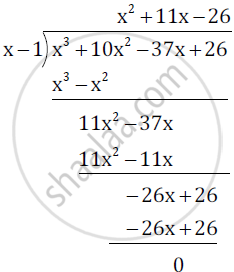
Thus by factor theorem
`=> x^3 + 10x^2 - 37x + 26 = (x - 1)(x^2 + 11x - 26)`
`= (x - 1) (x^2 + 13x - 2x - 26)`
`= (x - 1)(x(x + 13) - 2(x + 13))`
`=> x^3 + 10x^2 - 37x + 26 = (x - 1)(x + 13)(x - 2)`
APPEARS IN
RELATED QUESTIONS
Check whether 7 + 3x is a factor of 3x3 + 7x.
If x3 + ax2 + bx + 6 has x – 2 as a factor and leaves a remainder 3 when divided by x – 3, find the values of a and b.
What number should be subtracted from x3 + 3x2 – 8x + 14 so that on dividing it by x – 2, the remainder is 10?
Using the Remainder Theorem, factorise each of the following completely.
3x3 + 2x2 − 19x + 6
When the polynomial x3 + 2x2 – 5ax – 7 is divided by (x – 1), the remainder is A and when the polynomial x3 + ax2 – 12x + 16 is divided by (x + 2), the remainder is B. Find the value of ‘a’ if 2A + B = 0.
Divide the first polynomial by the second polynomial and find the remainder using remainder theorem.
(54m3 + 18m2 − 27m + 5) ; (m − 3)
Find without division, the remainder in the following :
x3 + 8x2 + 7x- 11 is divisible by (x+4)
Find the values of a and b when the polynomials f(x)= 2x2 -5x +a and g(x)= 2x2 + 5x +b both have a factor (2x+1).
Find the remainder when the polynomial f(x) = 2x4 - 6x3 + 2x2 - x + 2 is divided by x + 2.
Find ‘a’ if the two polynomials ax3 + 3x2 – 9 and 2x3 + 4x + a, leaves the same remainder when divided by x + 3.
