Advertisements
Advertisements
प्रश्न
Using the Remainder and Factor Theorem, factorise the following polynomial:
`x^3 + 10x^2 - 37x + 26`
उत्तर
`f(x) = x^3 + 10x^2 - 37x + 26`
For x = 1
`f(1) = (1)^2 + 10(1)^2 - 37(1) + 26`
= 1 + 10 - 37 + 26
= 0
=> (x - 1) is a factor of `x^3 + 10x^2 - 37x + 26`
Now
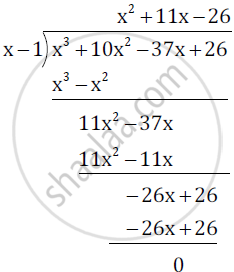
Thus by factor theorem
`=> x^3 + 10x^2 - 37x + 26 = (x - 1)(x^2 + 11x - 26)`
`= (x - 1) (x^2 + 13x - 2x - 26)`
`= (x - 1)(x(x + 13) - 2(x + 13))`
`=> x^3 + 10x^2 - 37x + 26 = (x - 1)(x + 13)(x - 2)`
APPEARS IN
संबंधित प्रश्न
Find the remainder when x3 + 3x2 – 12x + 4 is divided by x – 2.
Use the Remainder Theorem to find which of the following is a factor of 2x3 + 3x2 – 5x – 6.
x + 1
Find without division, the remainder in the following :
x3 + 8x2 + 7x- 11 is divisible by (x+4)
A polynomial f(x) when divided by (x - 1) leaves a remainder 3 and when divided by (x - 2) leaves a remainder of 1. Show that when its divided by (x - i)(x - 2), the remainder is (-2x + 5).
When x3 – 3x2 + 5x – 7 is divided by x – 2,then the remainder is
If on dividing 4x2 – 3kx + 5 by x + 2, the remainder is – 3 then the value of k is
Find the remainder when 2x3 – 3x2 + 4x + 7 is divided by x – 2
When a polynomial f(x) is divided by (x – 1), the remainder is 5 and when it is,, divided by (x – 2), the remainder is 7. Find – the remainder when it is divided by (x – 1) (x – 2).
Without actual division, prove that 2x4 – 5x3 + 2x2 – x + 2 is divisible by x2 – 3x + 2. [Hint: Factorise x2 – 3x + 2]
4x2 – kx + 5 leaves a remainder 2 when divided by x – 1. The value of k is ______.
