Advertisements
Advertisements
Question
When an alternating voltage of 220V is applied across device X, a current of 0.25A flows which lags behind the applied voltage in phase by π/2 radian. If the same voltage is applied across another device Y, the same current flows but now it is in phase with the applied voltage.
- Name the devices X and Y.
- Calculate the current flowing in the circuit when the same voltage is applied across the series combination of X and Y.
Solution
(i) In device X, the Current lags behind the voltage by π/2, X is an inductor.
In device Y, Current in phase with the applied voltage, and Y is resistor.
(ii) We are given that,
Current = `"V"/"X"_"L"`
Or, `0.25 = 220/"X"_"L"`,
∴ XL = 880Ω
Again, Current = `"V"/"R"`
Or, `0.25 = 220/"R"`
∴ R = 880Ω
For the series combination of X and Y,
Equivalent impedance Z = `sqrt(880^2 + 880^2)`
Z = `880sqrt2Omega`
Current = `"V"/"Z"`
Or, I = `220/(880sqrt2)`
∴ I = 0.177 A
APPEARS IN
RELATED QUESTIONS
A series LCR circuit is connected to a source having voltage v = vm sin ωt. Derive the expression for the instantaneous current I and its phase relationship to the applied voltage.
Obtain the condition for resonance to occur. Define ‘power factor’. State the conditions under which it is (i) maximum and (ii) minimum.
An inductor-coil of resistance 10 Ω and inductance 120 mH is connected across a battery of emf 6 V and internal resistance 2 Ω. Find the charge which flows through the inductor in (a) 10 ms, (b) 20 ms and (c) 100 ms after the connections are made.
Answer the following question.
What is the phase difference between the voltages across the inductor and the capacitor at resonance in the LCR circuit?
Choose the correct answer from given options
The phase difference between the current and the voltage in series LCR circuit at resonance is
Keeping the source frequency equal to the resonating frequency of the series LCR circuit, if the three elements, L, C and R are arranged in parallel, show that the total current in the parallel LCR circuit is minimum at this frequency. Obtain the current rms value in each branch of the circuit for the elements and source specified for this frequency.
If an LCR series circuit is connected to an ac source, then at resonance the voltage across ______.
In series LCR circuit, the phase angle between supply voltage and current is ______.
As the frequency of an ac circuit increases, the current first increases and then decreases. What combination of circuit elements is most likely to comprise the circuit?
- Inductor and capacitor.
- Resistor and inductor.
- Resistor and capacitor.
- Resistor, inductor and capacitor.
Consider the LCR circuit shown in figure. Find the net current i and the phase of i. Show that i = v/Z`. Find the impedance Z for this circuit.
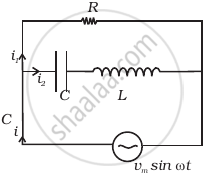
For an LCR circuit driven at frequency ω, the equation reads
`L (di)/(dt) + Ri + q/C = v_i = v_m` sin ωt
- Multiply the equation by i and simplify where possible.
- Interpret each term physically.
- Cast the equation in the form of a conservation of energy statement.
- Integrate the equation over one cycle to find that the phase difference between v and i must be acute.
