Advertisements
Advertisements
Question
Which of the following combinations have the same equivalent resistance between X and Y?
Options
Solution
Explanation:
1. In above first figure, the resistors are connected in parallel
Between X and Y.
Let Rp be their equivalent resistance.
Then,
`1/R_p=1/2+1/2`
`1/R_p=2/2`
Or, Rp = 1 Ω ...(i)
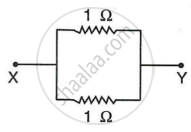
In the circuit there are three parts. In the first part two resistor of 1 Ω each are connected in series.
In series, the equivalent resistance is R'S, then
R'S = (1 + 1) Ω = 2 Ω
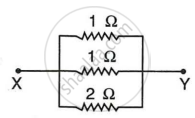
2. In the circuit, three resistors of 1 Ω, 1 Ω and 2 Ω are connected in parallel. In parallel, the equivalent resistance is RP, then
`1/"R"_"p" = 1/1 + 1/1 + 1/2`
`1/"R"_"p" = (2 + 2 + 1)/2`
`"R"_"p" = 2/5 Omega`
∴ RP = 0.4 Ω
Hence, RP = 0.4 Ω
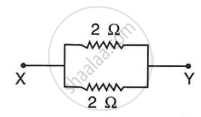
3. In the circuit two resistors of 1 Ω each are connected in parallel. In parallel, the equivalent resistance is RP, then
`1/"R"_"p" = 1/1 + 1/1`
`1/"R"_"p" = (1 + 1)/1`
`1/"R"_"p" = 2/1`
`"R"_"p" = 1/2`
∴ RP = 0.5 Ω
Hence, RP = 0.5 Ω
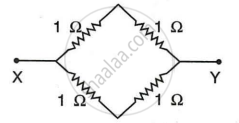
4. In the circuit there are three parts. In the first part two resistor of 1 Ω each are connected in series. In series, the equivalent resistance is R'S, then
R''S = (1 + 1) Ω = 2 Ω
In the third part, R'S and R''S are in parallel, the equivalent resistance is RP, then
`1/R_p=1/2+1/2`
`1/R_p=2/2`
Or, Rp = 1 Ω
Hence, RP = 1 Ω
Therefore, on observing the values we can say that first and fourth have same equivalent resistances i.e., 1 Ω.
APPEARS IN
RELATED QUESTIONS
Differentiate between resistances in series and parallel.
With a neat labelled diagram and derive the equation for three resistances connected in parallel.
Two resistors, with resistance 5 Ω and 10 Ω respectively are to be connected to a battery of emf 6 V so as to obtain:
(i) minimum current flowing
(ii) maximum current flowing
(a) How will you connect the resistances in each case?
(b) Calculate the strength of the total current in the circuit in the two cases.
A resistor of 8 ohms is connected in parallel with another resistor X. The resultant resistance of the combination is 4.8 ohms. What is the value of the resistor X?
State how are the two resistors joined with a battery when equivalent resistance is less than either of the two resistances.
A battery of e.m.f 16 V and internal resistance 2 Ω is connected to two resistors 3Ω and 6Ω connected in parallel. Find:
- the current through the battery.
- p.d. between the terminals of the battery,
- the current in 3 Ω resistors,
- the current in 6 Ω resistor.
The circuit diagram Fig shows three resistors 2 Ω, 4 Ω and R Ω connected to a battery of e.m.f. 2 V and internal resistance 3 Ω. If main current of 0.25 A flows through the circuit, find:
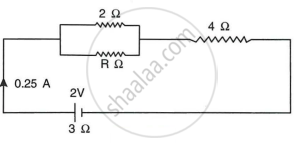
- the p.d. across the 4 Ω resistor,
- the p.d. across the internal resistance of the cell,
- the p.d. across the R Ω or 2 Ω resistors
- the value of R.
Two resistors of resistance 4 Ω and 6 Ω are connected in parallel to a cell to draw 0.5 A current from the cell.
Draw a labeled diagram of the arrangement
A current of 2 A is passed through a coil of resistance 75 Ω for 2 minutes.
(a) How much heat energy is produced?
(b) How much charge is passed through the resistance?
The least resistance obtained by using 2 Ω, 4 Ω, 1 Ω and 100 Ω is: