Advertisements
Advertisements
Question
याद कीजिए कि दो वृत्त सर्वांगसम होते हैं, यदि उनकी त्रिज्याएँ बराबर हों। सिद्ध कीजिए कि सर्वांगसम वृत्तों की बराबर जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करती हैं।
Solution
वृत्त उन बिंदुओं का समूह है जो एक स्थिर बिंदु से समान दूरी पर होते हैं। इस स्थिर बिंदु को वृत्त का केंद्र कहा जाता है और इस समान दूरी को वृत्त की त्रिज्या कहा जाता है। और इस प्रकार, वृत्त का आकार उसकी त्रिज्या पर निर्भर करता है। इसलिए, यह देखा जा सकता है कि यदि हम बराबर त्रिज्या वाले दो वृत्तों को एक दूसरे को आरोपित करने का प्रयास करते हैं, तो दोनों वृत्त एक दूसरे को ढक लेंगे। इसलिए, दो वृत्त सर्वांगसम होते हैं यदि उनकी त्रिज्या बराबर हो।
दो सर्वांगसम वृत्तों पर विचार कीजिए जिनके केंद्र O और O' हैं तथा बराबर लंबाई की दो जीवाएँ AB और CD हैं।
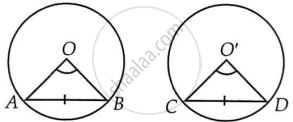
ΔAOB और ΔCO'D में,
AB = CD ...(बराबर लंबाई की जीवाएँ)
OA = O'C ...(सर्वांगसम वृत्तों की त्रिज्याएँ)
OB = O'D ...(सर्वांगसम वृत्तों की त्रिज्याएँ)
∴ ΔAOB ≅ ΔCO'D ...(SSS सर्वांगसमता नियम)
⇒ ∠AOB = ∠CO'D ...(CPCT से)
अतः, सर्वांगसम वृत्तों की बराबर जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करती हैं।
APPEARS IN
RELATED QUESTIONS
सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों की जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करें, तो जीवाएँ बराबर होती हैं।
यदि BM और CN त्रिभुज ABC की भुजाओं AC और AB पर खींचे गए लंब हैं, तो सिद्ध कीजिए कि बिंदु B, C, M और N चक्रीय हैं।
केंद्रों O और O' वाले दो वृत्त बिंदुओं A और B पर प्रतिच्छेद करते हैं। A (या B) से होकर एक रेखा PQ रेखाखंड OO' के समांतर खींची जाती है, जो वृत्तों को P और Q पर प्रतिच्छेद करती है। सिद्ध कीजिए कि PQ = 2 OO' है।
यदि P, Q और R क्रमश : एक त्रिभुज की BC, CA और AB भुजाओं के मध्य-बिंदु हैं तथा AD शीर्ष A से BC पर लंब है, तो सिद्ध कीजिए कि बिंदु P, Q, R और D चक्रीय है।
यदि एक चक्रीय चतुर्भुज ABCD के सम्मुख कोणों के समद्विभाजक इस चतुर्भुज के परिगत वृत्त को P और Q, बिंदुओं पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि PQ इस वृत्त का व्यास है।
