Advertisements
Advertisements
A certain number of metallic cones, each of radius 2 cm and height 3 cm are melted and recast into a solid sphere of radius 6 cm. Find the number of cones.
Concept: Surface Area of a Sphere
Solve the following inequation, write the solution set and represent it on the number line.
`-3(x - 7) >= 15 - 7x > (x+1)/3`, x ∉ R
Concept: Representation of Solution on the Number Line
Use graph paper for this question. (Take 2 cm = 1 unit along both x and y-axis.) Plot the points O(0, 0), A(-4, 4), B(-3, 0) and C(0, -3)
1) Reflect points A and B on the y-axis and name them A’ and B’ respectively. Write down their coordinates.
2) Name the figure OABCB’A’.
3) State the line of symmetry of this figure
Concept: Concept of Lines Symmetry
A model of a ship is made to a scale 1: 300
1) The length of the model of the ship is 2 m. Calculate the lengths of the ship.
2) The area of the deck ship is 180,000 m2. Calculate the area of the deck of the model.
3) The volume of the model in 6.5 m3. Calculate the volume of the ship.
Concept: Surface Area of a Sphere
A model of a ship is made to a scale 1: 300
1) The length of the model of the ship is 2 m. Calculate the lengths of the ship.
2) The area of the deck ship is 180,000 m2. Calculate the area of the deck of the model.
3) The volume of the model in 6.5 m3. Calculate the volume of the ship.
Concept: Surface Area of a Sphere
Solve the following inequation, write down the solution set and represent it on the real number line:
–2 + 10x ≤ 13x + 10 < 24 + 10x, x 𝜖 Z
Concept: Representation of Solution on the Number Line
On a map drawn to a scale of 1: 50,000, a rectangular plot of land ABCD has the following dimensions. AB = 6 cm; BC = 8 cm and all angles are right angles. Find:
1) the actual length of the diagonal distance AC of the plot in km.
2) the actual area of the plot in sq. km.
Concept: Surface Area of a Sphere
On a map drawn to a scale of 1: 50,000, a rectangular plot of land ABCD has the following dimensions. AB = 6 cm; BC = 8 cm and all angles are right angles. Find:
1) the actual length of the diagonal distance AC of the plot in km.
2) the actual area of the plot in sq. km.
Concept: Surface Area of a Sphere
The following figure represents a solid consisting of a right circular cylinder with a hemisphere at one end and a cone at the other. This common radius is 7 cm. The height of the cylinder and cone are each of 4 cm. Find the volume of the solid.

Concept: Surface Area of a Right Circular Cone
The following figure represents a solid consisting of a right circular cylinder with a hemisphere at one end and a cone at the other. This common radius is 7 cm. The height of the cylinder and cone are each of 4 cm. Find the volume of the solid.

Concept: Surface Area of a Right Circular Cone
Solve the following inequation and write the solution set:
13x – 5 < 15x + 4 < 7x + 12, x ∈ R
Represent the solution on a real number line.
Concept: Representation of Solution on the Number Line
In the given figure, ABCD is the square of side 21 cm. AC and BD are two diagonals of the square. Two semicircles are drawn with AD and BC as diameters. Find the area of the shaded region. (Take `pi = 22/7`)

Concept: Circle - Direct Application Problems Including Inner and Outer Area
Use a graph paper for this question taking 1 cm = 1 unit along both the x and y-axis :
1) Plot the points A(0, 5), B(2, 5), C(5, 2), D(5, -2), E(2, -5) and F(0, -5).
2) Reflect the points B, C, D and E on the y-axis and name them respectively as B’, C’, D’ and E’.
3) Write the coordinates of B’, C’, D’ and E’.
4) Name the figure formed by B C D E E’ D’ C’ B’.
5) Name a line of symmetry for the figure formed.
Concept: Concept of Lines Symmetry
Two solid spheres of radii 2 cm and 4 cm are melted and recast into a cone of height 8 cm. Find the radius of the cone so formed.
Concept: Surface Area of a Sphere
Two solid spheres of radii 2 cm and 4 cm are melted and recast into a cone of height 8 cm. Find the radius of the cone so formed.
Concept: Surface Area of a Sphere
Find the values of x, which satisfy the inequation `-2 5/6 < 1/2 - (2x)/3 ≤ 2, x ∈ W`. Graph the solution set on the number line.
Concept: Representation of Solution on the Number Line
In the figure given below, ABCD is the rectangle. AB = 14 cm, BC = 7 cm. From the rectangle, a quarter circle BFEC and a semicircle DGE are removed. Calculate the area of the remaining piece of the rectangle. (Take `pi = 22/7`).
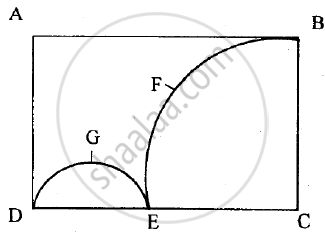
Concept: Circle - Direct Application Problems Including Inner and Outer Area
Use graph paper to answer the following questions. (Take 2 cm = 1 unit on both axes)
1) Plot the points A( -4, 2) and B(2, 4)
2) A' is the image of A when reflected at the y-axis. Plot it on the graph paper and write the coordinates of A'.
3) B' is the image of B when reflected on the line AA'. Write the coordinates of B'.
4) Write the geometric name of the figure ABA'B'.
5) Name a line of symmetry of the figure formed
Concept: Concept of Lines Symmetry
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate:
- the radius of the sphere.
- the number of cones recast. (Take π = `22/7`)
Concept: Surface Area of a Sphere
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate:
- the radius of the sphere.
- the number of cones recast. (Take π = `22/7`)
Concept: Surface Area of a Sphere
