Science (English Medium) Class 11 - CBSE Question Bank Solutions for Physics

The nearest star to our solar system is 4.29 light years away. How much is this distance in terms of parsecs? How much parallax would this star (named Alpha Centauri) show when viewed from two locations of the Earth six months apart in its orbit around the Sun?

When the planet Jupiter is at a distance of 824.7 million kilometres from the Earth, its angular diameter is measured to be 35.72″ of arc. Calculate the diameter of Jupiter

The position-time (x-t) graphs for two children A and B returning from their school O to their homes P and Q respectively, are shown in the figure. Choose the correct entries in the brackets below;

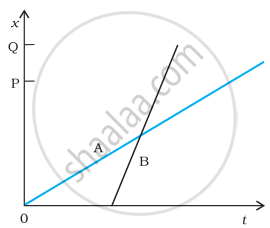
1. (A/B) lives closer to the school than (B/A)
2. (A/B) starts from the school earlier than (B/A)
3. (A/B) walks faster than (B/A)
4. A and B reach home at the (same/different) time
5. (A/B) overtakes (B/A) on the road (once/twice).

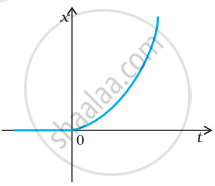
The figure shows the x-t plot of one-dimensional motion of a particle. Is it correct to say from the graph that the particle moves in a straight line for t < 0 and on a parabolic path for t > 0? If not, suggest a suitable physical context for this graph.

A police van moving on a highway with a speed of 30 km h^–1 fires a bullet at a thief’s car speeding away in the same direction with a speed of 192 km h^–1. If the muzzle speed of the bullet is 150 m s^–1, with what speed does the bullet hit the thief’s car? (Note: Obtain that speed which is relevant for damaging the thief’s car).

Just as precise measurements are necessary in science, it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations. Think of ways by which you can estimate the following (where an estimate is difficult to obtain, try to get an upper bound on the quantity):

the number of strands of hair on your head

Just as precise measurements are necessary in science, it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations. Think of ways by which you can estimate the following (where an estimate is difficult to obtain, try to get an upper bound on the quantity):-

the number of air molecules in your classroom.

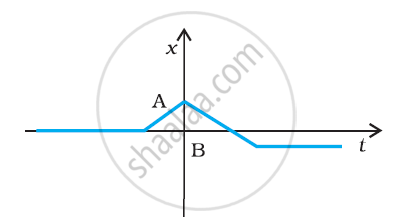
Suggest a suitable physical situation for the following graphs: 

State, for each of the following physical quantities, if it is a scalar or a vector: volume, mass, speed, acceleration, density, number of moles, velocity, angular frequency, displacement, angular velocity.

Pick out the two scalar quantities in the following list:

Force, Angular momentum, Work, Current, Linear momentum, Electric field, Average velocity, Magnetic moment, Relative velocity.

Pick out the only vector quantity in the following list:

State with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:

1. adding any two scalars,
2. adding a scalar to a vector of the same dimensions,
3. multiplying any vector by any scalar,
4. multiplying any two scalars,
5. adding any two vectors,
6. adding a component of a vector to the same vector.

Read the statement below carefully and state with reason, if it is true or false:

The magnitude of a vector is always a scalar.

Read the statement below carefully and state with reason, if it is true or false:

Each component of a vector is always a scalar.

Read the statement below carefully and state with reason, if it is true or false:

The total path length is always equal to the magnitude of the displacement vector of a particle. 

Read the statement below carefully and state with reason, if it is true or false: 

The average speed of a particle (defined as total path length divided by the time taken to cover the path) is either greater or equal to the magnitude of average velocity of the particle over the same interval of time.

Read the statement below carefully and state with reason, if it is true or false:

Three vectors not lying in a plane can never add up to give a null vector.

The position of a particle is given by

`r = 3.0t  hati − 2.0t 2  hatj + 4.0  hatk m`

Where t is in seconds and the coefficients have the proper units for r to be in metres.

1. Find the v and a of the particle?
2. What is the magnitude and direction of velocity of the particle at t = 2.0 s?

A vector has magnitude and direction. Does it have a location in space? Can it vary with time? Will two equal vectors a and b at different locations in space necessarily have identical physical effects? Give examples in support of your answer.

Can you associate vectors with (a) the length of a wire bent into a loop, (b) a plane area, (c) a sphere? Explain.