Advertisements
Advertisements
प्रश्न
100 और 200 के बीच के उन पूर्णांकों का योग ज्ञात कीजिए, जो
- 9 से विभाज्य हैं।
- 9 से विभाज्य नहीं हैं।
[संकेत (ii) : ये संख्याएँ होंगी : कुल संख्याएँ – 9 से विभाज्य संख्याएँ]
Advertisements
उत्तर
i. 100 और 200 के बीच की संख्याएँ (पूर्णांक) जो 9 से विभाज्य हैं, 108, 117, 126,..., 198 हैं।
मान लीजिए n 100 और 200 के बीच पदों की संख्या है जो 9 से विभाज्य है।
यहाँ, a = 108, d = 117 – 108 = 9 और an = l = 198
⇒ 198 = 108 + (n – 1)9 ...[∵ an = l = a + (n – 1)d]
⇒ 90 = (n – 1)9
⇒ n – 1 = 10
⇒ n = 11
∴ 100 और 200 के बीच के पदों का योग जो 9 से विभाज्य है।
Sn = `n/2[2a + (n - 1)d]`
⇒ S11 = `11/2[2(108) + (11 - 1)9]`
= `1/2[216 + 90]`
= `11/2 xx 306`
= 11 × 153
= 1683
अतः, 100 और 200 के बीच 9 से विभाज्य पूर्णांकों का आवश्यक योग 1683 है।
ii. 100 और 200 के बीच के पूर्णांकों का योग जो 9 से विभाज्य नहीं है = (100 और 200 के बीच की कुल संख्याओं का योग) – (100 और 200 के बीच की कुल संख्याओं का योग जो 9 से विभाज्य है) ...(i)
100 और 200 के बीच कुल संख्या 101, 102, 103,..., 199 है।
यहाँ, a = 101, d = 102 – 101 = 1 और an = l = 199
⇒ 199 = 101 + (n – 1)1 ...[∵ an = l = a + (n – 1)d]
⇒ (n – 1) = 98
⇒ n = 99
100 और 200 के बीच पदों का योग,
Sn = `n/2[2a + (n - 1)d]`
⇒ S99 = `99/2[2(101) + (99 - 1)1]`
= `99/2[202 + 98]`
= `99/2 xx 300`
= 99 × 150
= 14850
समीकरण (i) से, 100 और 200 के बीच पूर्णांकों का योग जो 9 से विभाज्य नहीं है।
= 14850 – 1683 ...[भाग (i) से]
= 13167
अतः, अभीष्ट योग 13167 है।
APPEARS IN
संबंधित प्रश्न
निम्नलिखित समांतर श्रेढ़ी का योग ज्ञात कीजिए:
2, 7, 12, ......,10 पदों तक
एक A.P. में, a12 = 37 और d = 3 दिया है। a और S12 ज्ञात कीजिए।
एक A.P. में, a = 8, an = 62 और Sn = 210 दिया है। n और d ज्ञात कीजिए।
एक A.P. में, an = 4, d = 2 और Sn = -14 दिया है। n और a ज्ञात कीजिए।
636 योग प्राप्त करने के लिए, AP.: 9, 17, 25, … के कितने पद लेने चाहिए?
निर्माण कार्य से संबंधित किसी ठेके में, एक निश्चित तिथि के बाद कार्य को विलंब से पूरा करने के लिए, जुर्माना लगाने का प्रावधान इस प्रकार हैं: पहले दिन के लिए ₹ 200, दूसरे दिन के लिए ₹ 250, तीसरे दिन के लिए ₹ 300 इत्यादि, अर्थात् प्रत्येक उत्तरोत्तर दिन का जुर्माना अपने से ठीक पहले दिन के जुर्माने से ₹ 50 अधिक है। एक ठेकेदार को जुर्माने के रूप में कितनी राशि अदा करनी पड़ेगी, यदि वह इस कार्य में 30 दिन का विलंब कर देता है?
केंद्र A से प्रारंभ करते हुए, बारी-बारी से केंद्रों A और B को लेते हुए, त्रिज्याओं 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm,……. वाले उतरोत्तर अर्धवृत्तों को खींचकर एक सर्पिल (Spiral) बनाया गया है, जैसाकि आकृति में दर्शाया गया है। तेरह क्रमागत अर्धवृत्तों से बने इस सर्पिल की कुल लंबाई क्या है? (π = `22/7` लीजिए।)
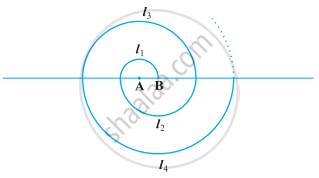
[संकेत: क्रमशः केंद्रों A, B, A, B,... वाले अर्धवृत्तों की लंबाइयाँ l1, l2, l3, l4 हैं।]
200 लट्ठों (logs) को ढेरी के रूप में इस प्रकार रखा जाता है : सबसे नीचे वाली पंक्ति में 20 लट्ठे, उससे अगली पंक्ति में 19 लट्ठे, उससे अगली पंक्ति में 18 लट्ठे, इत्यादि (देखिए आकृति)। ये 200 लठ्ठे कितनी पंक्तियों में रखे गए हैं तथा सबसे ऊपरी पंक्ति में कितने लट्ठे हैं?
योग ज्ञात कीजिए :
`4 - 1/"n" + 4 - 2/"n" + 4 - 3/"n" + ... + "n पदों तक"`
किसी AP के 11 वें पद का 18 वे पद से अनुपात 2 : 3 है। 5 वें पद का 21 वें पद से अनुपात ज्ञात कीजिए तथा साथ ही प्रथम पाँच पदों के योग का प्रथम 21 पदों के योग से अनुपात ज्ञात कीजिए।
