Advertisements
Advertisements
प्रश्न
123x2y – 138x2y is a like term of ______.
विकल्प
10xy
–15xy
–15xy2
10x2y
उत्तर
123x2y – 138x2y is a like term of `bb(underline(10x^2y))`.
Explanation:
123x2y – 138x2y = (123 – 138)x2y
= –15x2y
Therefore, –15x2y is a like term of 10x2y, because both contain x2y.
APPEARS IN
संबंधित प्रश्न
Identify like term in the following:
10pq, 7p, 8q, −p2q2, −7qp, −100q, −23, 12q2p2, −5p2, 41, 2405p, 78qp, 13p2q, qp2, 701p2
Take away:
\[\frac{y^3}{3} + \frac{7}{3} y^2 + \frac{1}{2}y + \frac{1}{2} \text { from } \frac{1}{3} - \frac{5}{3} y^2\]
Simplify the following:
\[\left( \frac{1}{3} y^2 - \frac{4}{7}y + 11 \right) - \left( \frac{1}{7}y - 3 + 2 y^2 \right) - \left( \frac{2}{7}y - \frac{2}{3} y^2 + 2 \right)\]
Find the product of the terms
3x2y , −3xy3, x2y2
The missing terms in the product −3m3n × 9(__) = _________ m4n3
Sum of a – b + ab, b + c – bc and c – a – ac is ______.
The product of two terms with unlike signs is a ______ term.
The product of two negative terms is a negative term.
The unlike terms in perimeters of following figures are ______ and ______.
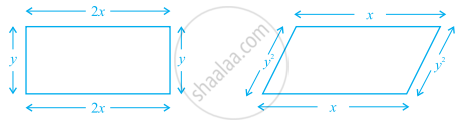
In like terms, variables and their powers are the same.
