Advertisements
Advertisements
प्रश्न
636 योग प्राप्त करने के लिए, AP.: 9, 17, 25, … के कितने पद लेने चाहिए?
उत्तर
इस A.P. के n पद होने दें।
इस A.P. के लिए, a = 9
d = a2 − a1
= 17 − 9
= 8
`S_n = n/2[2a+(n-1)d]`
`636 = n/2[2xx9+(-1)8]`
⇒ 636 = 9n + 4n2 - 4n
⇒ 4n2 + 5n - 636 = 0
⇒ 4n2 + 53n - 48n = 636 = 0
⇒ n(4n + 53) - 12(4n + 53) = 0
⇒ (4n + 53) (n - 12) = 0
⇒ 4n + 53 = 0 या n - 12 = 0
⇒ n = `(-53)/4` या n = 12
चूँकि पदों की संख्या न तो ऋणात्मक हो सकती है और न ही भिन्नात्मक, इसलिए, n = 12 ही होगा।
APPEARS IN
संबंधित प्रश्न
नीचे दिए गए योगफल को ज्ञात कीजिए:
`7 + 10 1/2 + 14 + ... + 84`
केंद्र A से प्रारंभ करते हुए, बारी-बारी से केंद्रों A और B को लेते हुए, त्रिज्याओं 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm,……. वाले उतरोत्तर अर्धवृत्तों को खींचकर एक सर्पिल (Spiral) बनाया गया है, जैसाकि आकृति में दर्शाया गया है। तेरह क्रमागत अर्धवृत्तों से बने इस सर्पिल की कुल लंबाई क्या है? (π = `22/7` लीजिए।)
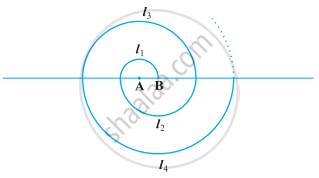
[संकेत: क्रमशः केंद्रों A, B, A, B,... वाले अर्धवृत्तों की लंबाइयाँ l1, l2, l3, l4 हैं।]
3 के प्रथम पाँच गुणजों का योग ______ है।
योग ज्ञात कीजिए :
1 + (–2) + (–5) + (–8) + ... + (–236)
योग ज्ञात कीजिए :
`(a - b)/(a + b) + (3a - 2b)/(a + b) + (5a - 3b)/(a + b) + ...` 11 पदों तक
AP: –2, –7, –12,... का कौन-सा पद –77 है? पद –77 तक इस AP का योग ज्ञात कीजिए।
उस AP के प्रथम 17 पदों का योग ज्ञात कीजिए, जिसके चौथे और 9 वें पद क्रमशः –15 और –30 हैं।
AP: −15, −13, −11,... का योग −55 बनाने के लिए इसके कितने पदों की आवश्यकता होगी? दो उत्तर प्राप्त होने का कारण स्पष्ट कीजिए।
ज्ञात कीजिए :
1 और 500 के बीच के उन पूर्णांकों का योग जो 2 के भी गुणज हैं और 5 के भी गुणज हैं।
ज्ञात कीजिए :
1 से 500 तक के उन पूर्णांकों का योग जो 2 या 5 के गुणज हैं।
[संकेत (iii) : ये संख्याएँ होंगी : 2 के गुणज + 5 के गुणज – 2 और 5 दोनों के गुणज]
