Advertisements
Advertisements
प्रश्न
A(-2, -3), B(-1, 0) and C(7, -6) are the vertices of a triangle. Find the circumcentre and the circumradius of the triangle.
उत्तर
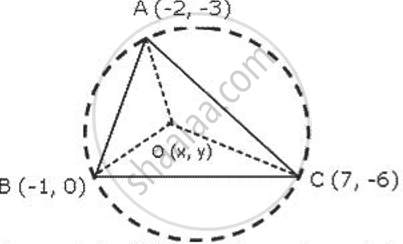
Circumcircle of MBCwill pass through the vertices A,B and C. AB = OB (radii of same circle)
⇒ OA2 =OB2
(x+2)2 +(y+3)2=(x+1)2 +Y2
⇒ 4x + 4 + 9 + 6y = 2x + 1
⇒ 2x+6y=-12 .....(1)
OB =OC (radii of same circle)
⇒ OB2 =OC2
(x + 1)2 + y2 =(x - 7)2 +(Y+ 6)2
⇒ 2x + 1= 49 - 144 x + 36 + 12
⇒ 16x - 12=8y
⇒ 4x - 3y = 21 ....(2)
On solving (1) and (2)
4x + 12y = -24
4x - 3y = 21
- + -
_____________
15 y = - 45
y = - 3
from (1)
2x + 6(-3) = -12
⇒ 2x = 6
⇒ x = 3
Circumcentre of Δ ABC is (3, - 3)and
Circumradius = `sqrt ((3 + 2)^2 + (-3 + 3)^2) = sqrt 25 = 5 "units"`
APPEARS IN
संबंधित प्रश्न
If P (2, – 1), Q(3, 4), R(–2, 3) and S(–3, –2) be four points in a plane, show that PQRS is a rhombus but not a square. Find the area of the rhombus
Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
If A (-1, 3), B (1, -1) and C (5, 1) are the vertices of a triangle ABC, find the length of the median through A.
Using the distance formula, show that the given points are collinear:
(6, 9), (0, 1) and (-6, -7)
Find the value of a if the distance between the points (5 , a) and (1 , 5) is 5 units .
P and Q are two points lying on the x - axis and the y-axis respectively . Find the coordinates of P and Q if the difference between the abscissa of P and the ordinates of Q is 1 and PQ is 5 units.
Find the coordinate of O , the centre of a circle passing through A (8 , 12) , B (11 , 3), and C (0 , 14). Also , find its radius.
Prove that the points (6 , -1) , (5 , 8) and (1 , 3) are the vertices of an isosceles triangle.
ABCD is a square . If the coordinates of A and C are (5 , 4) and (-1 , 6) ; find the coordinates of B and D.
The distance of the point P(–6, 8) from the origin is ______.
