Advertisements
Advertisements
प्रश्न
P(5 , -8) , Q (2 , -9) and R(2 , 1) are the vertices of a triangle. Find tyhe circumcentre and the circumradius of the triangle.
उत्तर
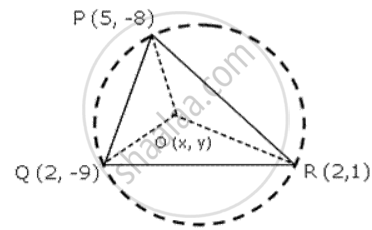
Circumcircle of Δ PQR will pass through its vertices P , Q and R.
OP = OQ
⇒ OP2 = OQ2
(x - 5)2 + (y + 8)2 = (x - 2)2 + (y + 9)2
⇒ 25 - 10x + 64 + 16y = 4 - 4x + 81 + 18 y
c - 6x - 2y + 4 =0
OQ = OR ...(radii of square circle)
OQ2 = OR2
(x - 2)2 + (y + 9)2 = (x - 2)2 + (y - 1)2
⇒ 81 + 18 y = 1 - 2y
⇒ 20 y = - 80
y = -4 ......(2)
-6x + 8+4 = 0 ......[from (2)]
⇒ -6x = -12
⇒ x = 2
Circumcentre of Δ PQR is O (2 , -4)
Circumcentre = `sqrt ((2 - 5)^2 + (-4 + 8)^2)`
`= sqrt (9 + 16) = sqrt 25` = 5 units
APPEARS IN
संबंधित प्रश्न
Two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of other two
vertices.
Find the distance between the following pairs of point.
W `((- 7)/2 , 4)`, X (11, 4)
Find the distance of a point (13 , -9) from another point on the line y = 0 whose abscissa is 1.
Find the distance between the following pairs of points:
(-3, 6) and (2, -6)
Find the distance between the origin and the point:
(8, -15)
A point P lies on the x-axis and another point Q lies on the y-axis.
If the abscissa of point P is -12 and the ordinate of point Q is -16; calculate the length of line segment PQ.
Points A (-3, -2), B (-6, a), C (-3, -4) and D (0, -1) are the vertices of quadrilateral ABCD; find a if 'a' is negative and AB = CD.
If the distance between point L(x, 7) and point M(1, 15) is 10, then find the value of x
The equation of the perpendicular bisector of line segment joining points A(4,5) and B(-2,3) is ______.
Find a point which is equidistant from the points A(–5, 4) and B(–1, 6)? How many such points are there?
