Advertisements
Advertisements
Question
P(5 , -8) , Q (2 , -9) and R(2 , 1) are the vertices of a triangle. Find tyhe circumcentre and the circumradius of the triangle.
Solution
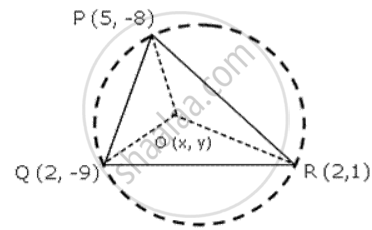
Circumcircle of Δ PQR will pass through its vertices P , Q and R.
OP = OQ
⇒ OP2 = OQ2
(x - 5)2 + (y + 8)2 = (x - 2)2 + (y + 9)2
⇒ 25 - 10x + 64 + 16y = 4 - 4x + 81 + 18 y
c - 6x - 2y + 4 =0
OQ = OR ...(radii of square circle)
OQ2 = OR2
(x - 2)2 + (y + 9)2 = (x - 2)2 + (y - 1)2
⇒ 81 + 18 y = 1 - 2y
⇒ 20 y = - 80
y = -4 ......(2)
-6x + 8+4 = 0 ......[from (2)]
⇒ -6x = -12
⇒ x = 2
Circumcentre of Δ PQR is O (2 , -4)
Circumcentre = `sqrt ((2 - 5)^2 + (-4 + 8)^2)`
`= sqrt (9 + 16) = sqrt 25` = 5 units
APPEARS IN
RELATED QUESTIONS
Show that the points (1, – 1), (5, 2) and (9, 5) are collinear.
Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
(- 1, - 2), (1, 0), (- 1, 2), (- 3, 0)
Find the distance of a point P(x, y) from the origin.
Determine whether the points are collinear.
A(1, −3), B(2, −5), C(−4, 7)
Distance of point (-3, 4) from the origin is .....
(A) 7 (B) 1 (C) 5 (D) 4
Given A = (3, 1) and B = (0, y - 1). Find y if AB = 5.
The distances of point P (x, y) from the points A (1, - 3) and B (- 2, 2) are in the ratio 2: 3.
Show that: 5x2 + 5y2 - 34x + 70y + 58 = 0.
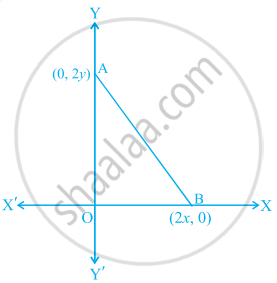
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.
Find the points on the x-axis which are at a distance of `2sqrt(5)` from the point (7, – 4). How many such points are there?
