Question

x (1,2),Y (3, -4) and z (5,-6) are the vertices of a triangle . Find the circumcentre and the circumradius of the triangle.

Answer 1

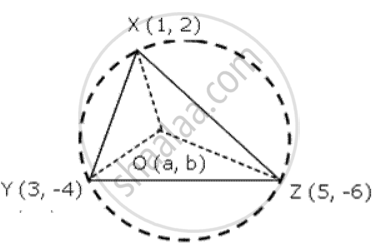
Circumcentre of Δ XYZ will pass through the vertices X , Y and Z

OX = OY    (radi of same circle),

⇒ OX² = OY²

(a - 1)² + (b - 2)² = (a - 3)² + (b + 4)²

⇒ 1 - 2a + 4 - 4b = 9 - 6a + 16 + 8b

⇒ 4a - 12b = 20

⇒ a - 3b = 5        .........(1)

OY = OZ   (radii of same circle)

OY² = OZ²

(a - 3)² + (b + 4)² = (a - 5)² + (b + 6)²

⇒ 9 - 6a + 16 + 8b = 25 - 10a + 36 + 12b

⇒ 4a - 4b = 36

⇒ a - b = 9        .........(2)

a - 3b = 5           ..........(1)

a - b = 9

- 2b = -4

b = 2

a = 11

Circumcentre of Δ XYZ is O (11 , 2)

Circumradius = `sqrt ((11 - 1)^2 + (2 - 2)^2) = sqrt 100` = 10 units