Advertisements
Advertisements
प्रश्न
P(5 , -8) , Q (2 , -9) and R(2 , 1) are the vertices of a triangle. Find tyhe circumcentre and the circumradius of the triangle.
उत्तर
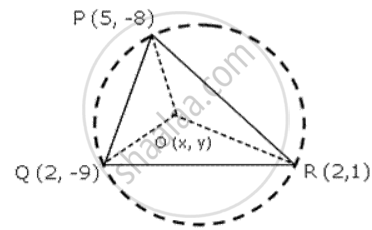
Circumcircle of Δ PQR will pass through its vertices P , Q and R.
OP = OQ
⇒ OP2 = OQ2
(x - 5)2 + (y + 8)2 = (x - 2)2 + (y + 9)2
⇒ 25 - 10x + 64 + 16y = 4 - 4x + 81 + 18 y
c - 6x - 2y + 4 =0
OQ = OR ...(radii of square circle)
OQ2 = OR2
(x - 2)2 + (y + 9)2 = (x - 2)2 + (y - 1)2
⇒ 81 + 18 y = 1 - 2y
⇒ 20 y = - 80
y = -4 ......(2)
-6x + 8+4 = 0 ......[from (2)]
⇒ -6x = -12
⇒ x = 2
Circumcentre of Δ PQR is O (2 , -4)
Circumcentre = `sqrt ((2 - 5)^2 + (-4 + 8)^2)`
`= sqrt (9 + 16) = sqrt 25` = 5 units
APPEARS IN
संबंधित प्रश्न
Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in Section 7.2.
Find the distance of the following points from the origin:
(ii) B(-5,5)
Using the distance formula, show that the given points are collinear:
(-1, -1), (2, 3) and (8, 11)
If P (x , y ) is equidistant from the points A (7,1) and B (3,5) find the relation between x and y
Find the distance of the following point from the origin :
(5 , 12)
Point P (2, -7) is the centre of a circle with radius 13 unit, PT is perpendicular to chord AB and T = (-2, -4); calculate the length of AB.

The points A (3, 0), B (a, -2) and C (4, -1) are the vertices of triangle ABC right angled at vertex A. Find the value of a.
Find the distance of the following points from origin.
(5, 6)
Show that the points (a, a), (-a, -a) and `(-asqrt(3), asqrt(3))` are the vertices of an equilateral triangle.
|
In a GPS, The lines that run east-west are known as lines of latitude, and the lines running north-south are known as lines of longitude. The latitude and the longitude of a place are its coordinates and the distance formula is used to find the distance between two places. The distance between two parallel lines is approximately 150 km. A family from Uttar Pradesh planned a round trip from Lucknow (L) to Puri (P) via Bhuj (B) and Nashik (N) as shown in the given figure below.
|
Based on the above information answer the following questions using the coordinate geometry.
- Find the distance between Lucknow (L) to Bhuj (B).
- If Kota (K), internally divide the line segment joining Lucknow (L) to Bhuj (B) into 3 : 2 then find the coordinate of Kota (K).
- Name the type of triangle formed by the places Lucknow (L), Nashik (N) and Puri (P)
[OR]
Find a place (point) on the longitude (y-axis) which is equidistant from the points Lucknow (L) and Puri (P).

