Advertisements
Advertisements
Question
A(-2, -3), B(-1, 0) and C(7, -6) are the vertices of a triangle. Find the circumcentre and the circumradius of the triangle.
Solution
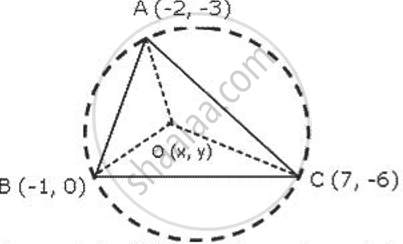
Circumcircle of MBCwill pass through the vertices A,B and C. AB = OB (radii of same circle)
⇒ OA2 =OB2
(x+2)2 +(y+3)2=(x+1)2 +Y2
⇒ 4x + 4 + 9 + 6y = 2x + 1
⇒ 2x+6y=-12 .....(1)
OB =OC (radii of same circle)
⇒ OB2 =OC2
(x + 1)2 + y2 =(x - 7)2 +(Y+ 6)2
⇒ 2x + 1= 49 - 144 x + 36 + 12
⇒ 16x - 12=8y
⇒ 4x - 3y = 21 ....(2)
On solving (1) and (2)
4x + 12y = -24
4x - 3y = 21
- + -
_____________
15 y = - 45
y = - 3
from (1)
2x + 6(-3) = -12
⇒ 2x = 6
⇒ x = 3
Circumcentre of Δ ABC is (3, - 3)and
Circumradius = `sqrt ((3 + 2)^2 + (-3 + 3)^2) = sqrt 25 = 5 "units"`
APPEARS IN
RELATED QUESTIONS
If A(4, 3), B(-1, y) and C(3, 4) are the vertices of a right triangle ABC, right-angled at A, then find the value of y.
In a classroom, 4 friends are seated at the points A, B, C and D as shown in the following figure. Champa and Chameli walk into the class and after observing for a few minutes, Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees.
Using distance formula, find which of them is correct.

Find the point on the x-axis which is equidistant from (2, -5) and (-2, 9).
Two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of other two
vertices.
Find the distance between the points
P(a + b,a - b)andQ(a -b,a + b)
Find a point on the y-axis which is equidistant from the points (5, 2) and (-4, 3).
Calculate the distance between A (7, 3) and B on the x-axis whose abscissa is 11.
The distance of the point P(–6, 8) from the origin is ______.
Point P(0, 2) is the point of intersection of y-axis and perpendicular bisector of line segment joining the points A(–1, 1) and B(3, 3).
The point A(2, 7) lies on the perpendicular bisector of line segment joining the points P(6, 5) and Q(0, – 4).
