Advertisements
Advertisements
प्रश्न
A, B और C किसी वृत्त पर स्थित तीन बिंदु हैं। सिद्ध कीजिए कि AB, BC और CA के लंब समद्विभाजक संगामी है।
उत्तर
दिया गया है - A, B और C एक वृत्त पर तीन बिंदु हैं।
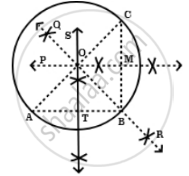
सिद्ध करना है - AB, BC और CA का लंब समद्विभाजक।
रचना - AB का ST, BC का PM और CA का QR लम्ब समद्विभाजक खींचिए। AB, BC और CA को मिलाइए।
उपपत्ति - OA = OB ...(i) [O, ST पर स्थित है, AB का लंब समद्विभाजक]
पुनः, OB = OC ...(ii) [O, PM पर स्थित है जो BC का लम्ब समद्विभाजक है।]
और OC = OA ...(iii) [O, QR पर स्थित है, CA का लम्ब समद्विभाजक]
अब, समीकरणों (i), (ii) और (iii) से,
OA = OB = OC = r
इसलिए, केंद्र O और त्रिज्या r के साथ एक वृत्त बनाएं, जो A, B और C से होकर गुजरेगा।
इसका अर्थ है बिंदु A, B और C से होकर जाने वाला एक वृत्त। चूंकि, ST, PM या QR एक दूसरे को एक और केवल एक बिंदु O पर काट सकते हैं।
इसलिए, केवल O ही एक ऐसा बिंदु है जो A, B और C से समान दूरी पर है।
अतः, AB, BC और CA के लंब समद्विभाजक संगामी हैं।
APPEARS IN
संबंधित प्रश्न
केंद्र O वाले वृत्त की दो जीवाएँ AB और AC, OA के विपरीत ओर स्थित हैं। तब, ∠OAB = ∠OAC है।
ABCD एक समांतर चतुर्भुज है। A और B से होकर एक वृत्त इस प्रकार खींचा जाता है कि वह AD को P पर और BC को Q पर प्रतिच्छेद करता है। सिद्ध कीजिए कि P, Q, C और D चक्रीय है।
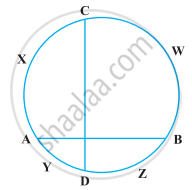
यदि किसी वृत्त AYDZBWCX की दो जीवाएँ AB और CD समकोण पर प्रतिच्छेद करती हैं (आकृति), तो सिद्ध कीजिए कि चाप CXA + चाप DZB = चाप AYD + चाप BWC = एक अर्धवृत्त है।