Advertisements
Advertisements
प्रश्न
A boy throws a ball in air at 60° to the horizontal along a road with a speed of 10 m/s (36 km/h). Another boy sitting in a passing by car observes the ball. Sketch the motion of the ball as observed by the boy in the car, if car has a speed of (18 km/h). Give explanation to support your diagram.
उत्तर
The situation is shown in the below diagram.
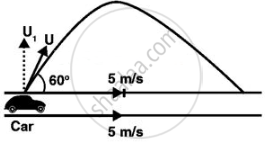
According to the problem, the boy standing on the ground throws the ball at an angle of 60° horizontal at a speed of 10 m/s.
∴ The horizontal component of velocity, ux = 10 cos θ
ux = (10 m/s) cos 60° = `10 xx 1/2` = 5 m/s
The vertical component of velocity, uy = 10 sin θ
uy = (10 m/s) sin 60° = `10 xx sqrt(3)/2 = 5sqrt(3)` m/s
Speed of the car = 18 km/h = 5 m/s
As the horizontal speed of ball and car is same, hence the relative velocity of ball w.r.t car in the horizontal direction will be zero.
Only the vertical motion of the ball will be observed by the boy in the car, as shown in the above diagram.
APPEARS IN
संबंधित प्रश्न
An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0 s a part is 30°, what is the speed of the aircraft?
A cricket ball thrown across a field is at heights h1 and h2 from the point of projection at times t1 and t2 respectively after the throw. The ball is caught by a fielder at the same height as that of projection. The time of flight of the ball in this journey is
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
A car starts from rest and accelerates at 5 m/s2. At t = 4 s, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at t = 6 s? (Take g = 10 m/s2)
Two particles are projected in air with speed vo at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then tick the right choices
- Angle of projection: q1 > q2
- Time of flight: T1 > T2
- Horizontal range: R1 > R2
- Total energy: U1 > U2
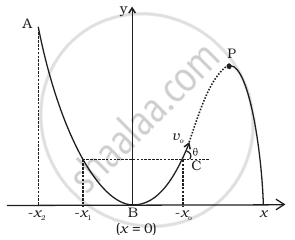
A particle slides down a frictionless parabolic (y = x2) track (A – B – C) starting from rest at point A (Figure). Point B is at the vertex of parabola and point C is at a height less than that of point A. After C, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then
A fighter plane is flying horizontally at an altitude of 1.5 km with speed 720 km/h. At what angle of sight (w.r.t. horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target?
A football is kicked into the air vertically upwards. What is its velocity at the highest point?
If a baseball player can throw a ball at maximum distance = d over a ground, the maximum vertical height to which he can throw it, will be (Ball has same initial speed in each case):
A ball is projected from the ground with a speed 15 ms-1 at an angle θ with horizontal so that its range and maximum height are equal, then tan θ will be equal to ______.
