Advertisements
Advertisements
प्रश्न
A chemist has a compound to be made using 3 basic elements X, Y, Z so that it has at least 10 litres of X, 12 litres of Y and 20 litres of Z. He makes this compound by mixing two compounds (I) and (II). Each unit compound (I) had 4 litres of X, 3 litres of Y. Each unit compound (II) had 1 litre of X, 2 litres of Y and 4 litres of Z. The unit costs of compounds (I) and (II) are ₹ 400 and ₹ 600 respectively. Find the number of units of each compound to be produced so as to minimize the cost
उत्तर
Let the chemist produce x units of compound I and y units of compound II.
Since x and y cannot be negative, x ≥ 0, y ≥ 0
The unit costs of compounds I and II are ₹ 400 and ₹ 600 respectively.
Total Cost = Z = 400x + 600y
We construct a table with constraints of X, Y and Z as follows:
| Compound I | Compound II | Least value | |
| X | 4 | 1 | 10 |
| Y | 3 | 2 | 12 |
| Z | – | 4 | 20 |
From the table, the constraints are
4x + y ≥ 10
3x + 2y ≥ 12
4y ≥ 20
∴ Given problem can be formulated as follows:
Minimize Z = 400x + 600y
Subject to 4x + y ≥ 10
3x + 2y ≥ 12
4y ≥ 20, x ≥ 0, y ≥ 0
To draw the feasible region, construct table as follows:
| Inequality | 4x + y ≥ 10 | 3x + 2y ≥ 12 | 4y ≥ 20 |
| Corresponding equation (of line) | 4x + y = 10 | 3x + 2y = 12 | 4y = 20 |
| Intersection of line with X-axis | `(5/2, 0)` | (4, 0) | – |
| Intersection of line with Y-axis | (0, 10) | (0, 6) | (0, 5) |
| Region | Non-Origin side | Non-Origin side | Non-Origin side |
Shaded portion EABY is the feasible region, whose vertices are A and B(0, 10).
A is the point of intersection of the lines 4y = 20 and 4x + y = 10,
Solving the above equations, we get
x = `5/4`, y = 5
∴ A ≡ `(5/4, 5)`
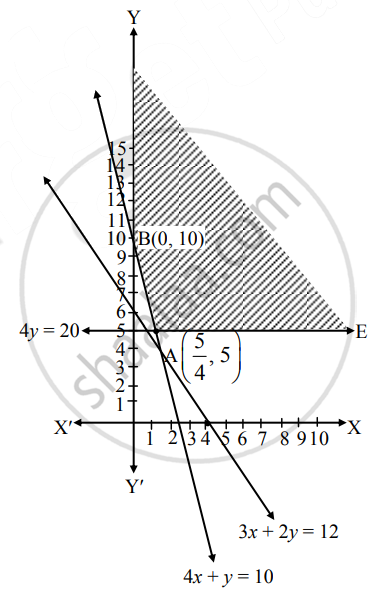
Here, the objective function is
Z = 400x + 600y
∴ Z at A`(5/4, 5) = 400(5/4) + 600(5)`
= 500 + 3000
= 3500
Z at B (0, 10) = 400(0) + 600(10)
= 6000
∴ Z has minimum value 3500 at x = `5/4` and y = 5.
∴ The chemist should produce `5/4` units of compound I and 5 units of compound II to minimize the cost.
APPEARS IN
संबंधित प्रश्न
A firm manufactures 3 products A, B and C. The profits are Rs 3, Rs 2 and Rs 4 respectively. The firm has 2 machines and below is the required processing time in minutes for each machine on each product :
| Machine | Products | ||
| A | B | C | |
| M1 M2 |
4 | 3 | 5 |
| 2 | 2 | 4 | |
Machines M1 and M2 have 2000 and 2500 machine minutes respectively. The firm must manufacture 100 A's, 200 B's and 50 C's but not more than 150 A's. Set up a LPP to maximize the profit.
The corner points of the feasible region determined by the following system of linear inequalities:
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both (3, 4) and (0, 5) is
Solve the following L.P.P. by graphical method:
Maximize: Z = 10x + 25y
subject to 0 ≤ x ≤ 3,
0 ≤ y ≤ 3,
x + y ≤ 5.
Also find the maximum value of z.
Solve the following L.P.P. by graphical method :
Maximize: Z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0 also find maximum value of Z.
Choose the correct alternative:
The value of objective function is maximize under linear constraints.
Choose the correct alternative :
The maximum value of z = 5x + 3y. subject to the constraints
Fill in the blank :
Graphical solution set of the in equations x ≥ 0, y ≥ 0 is in _______ quadrant
The constraint that a factory has to employ more women (y) than men (x) is given by _______
Solve the following problem :
Maximize Z = 5x1 + 6x2 Subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x ≥ 0, x2 ≥ 0
Solve the following problem :
Minimize Z = 4x + 2y Subject to 3x + y ≥ 27, x + y ≥ 21, x ≥ 0, y ≥ 0
Solve the following problem :
A Company produces mixers and processors Profit on selling one mixer and one food processor is ₹ 2000 and ₹ 3000 respectively. Both the products are processed through three machines A, B, C The time required in hours by each product and total time available in hours per week on each machine are as follows:
| Machine/Product | Mixer per unit | Food processor per unit | Available time |
| A | 3 | 3 | 36 |
| B | 5 | 2 | 50 |
| C | 2 | 6 | 60 |
How many mixers and food processors should be produced to maximize the profit?
Solve the following problem :
A firm manufacturing two types of electrical items A and B, can make a profit of ₹ 20 per unit of A and ₹ 30 per unit of B. Both A and B make use of two essential components, a motor and a transformer. Each unit of A requires 3 motors and 2 transformers and each unit of B requires 2 motors and 4 transformers. The total supply of components per month is restricted to 210 motors and 300 transformers. How many units of A and B should be manufacture per month to maximize profit? How much is the maximum profit?
Choose the correct alternative:
If LPP has optimal solution at two point, then
Choose the correct alternative:
The maximum value of Z = 3x + 5y subjected to the constraints x + y ≤ 2, 4x + 3y ≤ 12, x ≥ 0, y ≥ 0 is
Choose the correct alternative:
The point at which the maximum value of Z = 4x + 6y subject to the constraints 3x + 2y ≤ 12, x + y ≥ 4, x ≥ 0, y ≥ 0 is obtained at the point
State whether the following statement is True or False:
Of all the points of feasible region, the optimal value is obtained at the boundary of the feasible region
A company manufactures two types of ladies dresses C and D. The raw material and labour available per day is given in the table.
| Resources | Dress C(x) | Dress D(y) | Max. availability |
| Raw material | 5 | 4 | 60 |
| Labour | 5 | 3 | 50 |
P is the profit, if P = 50x + 100y, solve this LPP to find x and y to get the maximum profit
Maximize Z = 2x + 3y subject to constraints
x + 4y ≤ 8, 3x + 2y ≤ 14, x ≥ 0, y ≥ 0.
Minimize Z = 2x + 3y subject to constraints
x + y ≥ 6, 2x + y ≥ 7, x + 4y ≥ 8, x ≥ 0, y ≥ 0
