Advertisements
Advertisements
प्रश्न
A wholesale dealer deals in two kinds of mixtures A and B of nuts. Each kg of mixture A contains 60 grams of almonds, 30 grams of cashew and 30 grams of hazel nuts. Each kg of mixture B contains 30 grams of almonds, 60 grams of cashew and 180 grams of hazel nuts. A dealer is contemplating to use mixtures A and B to make a bag which will contain at least 240 grams of almonds, 300 grams of cashew and 540 grams of hazel nuts. Mixture A costs ₹ 8 and B costs ₹ 12 per kg. How many kgs of each mixture should he use to minimize the cost of the kgs
Advertisements
उत्तर
Let the dealer use x kg of mixture A and y kg of mixture B.
Since x and y cannot be negative, x ≥ 0, y ≥ 0
Mixture A costs ₹ 8 and Mixture B costs ₹ 12 per kg.
∴ Total cost = Z = 8x + 12y
We construct a table with the constraints of Almond, Cashew and Hazelnut as follows:
| Mixture A | Mixture B | Least value | |
| Almond | 60 | 30 | 240 |
| Cashew | 30 | 60 | 300 |
| Hazelnut | 30 | 180 | 540 |
From the table, the constraints are
60x + 30y ≥ 240
30x + 60y ≥ 300
30x + 180y ≥ 540
∴ Given problem can be formulated as follows:
Minimize Z = 8x + 12y
Subject to 60x + 30y ≥ 240
30x + 60y ≥ 300
30x + 180y ≥ 540, x ≥ 0, y ≥ 0
To draw the feasible region, construct table as follows:
| Inequality | 60x +30y ≥ 240 | 30x+ 60y ≥ 300 | 30x+ 180y ≥ 540 |
| Corresponding equation (of line) | 60x+ 30y = 240 | 30x + 60y = 300 | 30x+ 180y = 540 |
| Intersection of line with X-axis | (4, 0) | (10, 0) | (18, 0) |
| Intersection of line with Y-axis | (0, 8) | (0, 5) | (0, 3) |
| Region | Non-origin side | Non-origin side | Non-origin side |
Shaded portion XABCDY is the feasible region, whose vertices are A(18, 0), B, C and D(0, 8).
B is the point of intersection of the lines 30x + 180y = 540 and 30x + 60y = 300.
Solving the above equations, we get
x = 6, y = 2
∴ B ≡ (6, 2)
C is the point of intersection of the lines 60x + 30y = 240 and 30x + 60y = 300.
Solving the above equations, we get
x = 2, y = 4
∴ C ≡ (2, 4)
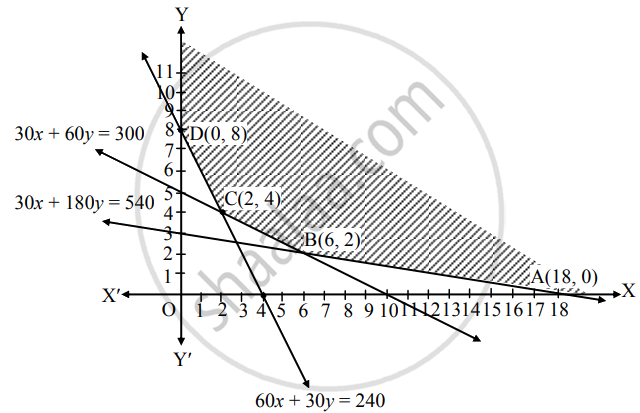
Here, the objective function is
Z = 8x + 12y
∴ Z at A(18, 0) = 8(18) + 12(0)
= 144
Z at B(6, 2) = 8(6) + 12(2)
= 48 + 24
= 72
Z at C(2, 4) = 8(2) + 12(4)
= 16 + 48
= 64
Z at D(0, 8) = 8(0) + 12(8)
= 96
∴ Z has minimum value 64 at x = 2 and y = 4.
∴ 2 kgs of mixture A and 4 kgs of mixture B should be used to minimize the cost of the kgs.
APPEARS IN
संबंधित प्रश्न
The postmaster of a local post office wishes to hire extra helpers during the Deepawali season, because of a large increase in the volume of mail handling and delivery. Because of the limited office space and the budgetary conditions, the number of temporary helpers must not exceed 10. According to past experience, a man can handle 300 letters and 80 packages per day, on the average, and a woman can handle 400 letters and 50 packets per day. The postmaster believes that the daily volume of extra mail and packages will be no less than 3400 and 680 respectively. A man receives Rs 225 a day and a woman receives Rs 200 a day. How many men and women helpers should be hired to keep the pay-roll at a minimum ? Formulate an LPP and solve it graphically.
A farmer has a 100 acre farm. He can sell the tomatoes, lettuce, or radishes he can raise. The price he can obtain is Rs 1 per kilogram for tomatoes, Rs 0.75 a head for lettuce and Rs 2 per kilogram for radishes. The average yield per acre is 2000 kgs for radishes, 3000 heads of lettuce and 1000 kilograms of radishes. Fertilizer is available at Rs 0.50 per kg and the amount required per acre is 100 kgs each for tomatoes and lettuce and 50 kilograms for radishes. Labour required for sowing, cultivating and harvesting per acre is 5 man-days for tomatoes and radishes and 6 man-days for lettuce. A total of 400 man-days of labour are available at Rs 20 per man-day. Formulate this problem as a LPP to maximize the farmer's total profit.
Solve the following LPP by graphical method:
Maximize z = 11x + 8y, subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0
Solve the following L.P.P. by graphical method :
Maximize : Z = 7x + 11y subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Choose the correct alternative:
The value of objective function is maximize under linear constraints.
Fill in the blank :
Graphical solution set of the in equations x ≥ 0, y ≥ 0 is in _______ quadrant
Fill in the blank :
The region represented by the in equations x ≤ 0, y ≤ 0 lines in _______ quadrants.
The region represented by the inequality y ≤ 0 lies in _______ quadrants.
The region represented by the inequalities x ≥ 0, y ≥ 0 lies in first quadrant.
Graphical solution set of x ≤ 0, y ≥ 0 in xy system lies in second quadrant.
Solve the following problem :
A company manufactures bicyles and tricycles, each of which must be processed through two machines A and B Maximum availability of machine A and B is respectively 120 and 180 hours. Manufacturing a bicycle requires 6 hours on machine A and 3 hours on machine B. Manufacturing a tricycle requires 4 hours on machine A and 10 hours on machine B. If profits are ₹ 180 for a bicycle and ₹ 220 on a tricycle, determine the number of bicycles and tricycles that should be manufacturing in order to maximize the profit.
Solve the following problem :
A firm manufacturing two types of electrical items A and B, can make a profit of ₹ 20 per unit of A and ₹ 30 per unit of B. Both A and B make use of two essential components, a motor and a transformer. Each unit of A requires 3 motors and 2 transformers and each unit of B requires 2 motors and 4 transformers. The total supply of components per month is restricted to 210 motors and 300 transformers. How many units of A and B should be manufacture per month to maximize profit? How much is the maximum profit?
Choose the correct alternative:
If LPP has optimal solution at two point, then
Choose the correct alternative:
The minimum value of Z = 4x + 5y subjected to the constraints x + y ≥ 6, 5x + y ≥ 10, x, y ≥ 0 is
Choose the correct alternative:
The corner points of the feasible region are (0, 3), (3, 0), (8, 0), `(12/5, 38/5)` and (0, 10), then the point of maximum Z = 6x + 4y = 48 is at
State whether the following statement is True or False:
A convex set includes the points but not the segment joining the points
State whether the following statement is True or False:
If the corner points of the feasible region are `(0, 7/3)`, (2, 1), (3, 0) and (0, 0), then the maximum value of Z = 4x + 5y is 12
If the feasible region is bounded by the inequations 2x + 3y ≤ 12, 2x + y ≤ 8, 0 ≤ x, 0 ≤ y, then point (5, 4) is a ______ of the feasible region
A company manufactures two types of ladies dresses C and D. The raw material and labour available per day is given in the table.
| Resources | Dress C(x) | Dress D(y) | Max. availability |
| Raw material | 5 | 4 | 60 |
| Labour | 5 | 3 | 50 |
P is the profit, if P = 50x + 100y, solve this LPP to find x and y to get the maximum profit
Smita is a diet conscious house wife, wishes to ensure certain minimum intake of vitamins A, B and C for the family. The minimum daily needs of vitamins A, B, and C for the family are 30, 20, and 16 units respectively. For the supply of the minimum vitamin requirements Smita relies on 2 types of foods F1 and F2. F1 provides 7, 5 and 2 units of A, B, C vitamins per 10 grams and F2 provides 2, 4 and 8 units of A, B and C vitamins per 10 grams. F1 costs ₹ 3 and F2 costs ₹ 2 per 10 grams. How many grams of each F1 and F2 should buy every day to keep her food bill minimum
Maximize Z = 400x + 500y subject to constraints
x + 2y ≤ 80, 2x + y ≤ 90, x ≥ 0, y ≥ 0
Minimize Z = 24x + 40y subject to constraints
6x + 8y ≥ 96, 7x + 12y ≥ 168, x ≥ 0, y ≥ 0
Minimize Z = x + 4y subject to constraints
x + 3y ≥ 3, 2x + y ≥ 2, x ≥ 0, y ≥ 0
Minimize Z = 2x + 3y subject to constraints
x + y ≥ 6, 2x + y ≥ 7, x + 4y ≥ 8, x ≥ 0, y ≥ 0
Solve the LPP graphically:
Minimize Z = 4x + 5y
Subject to the constraints 5x + y ≥ 10, x + y ≥ 6, x + 4y ≥ 12, x, y ≥ 0
Solution: Convert the constraints into equations and find the intercept made by each one of it.
| Inequations | Equations | X intercept | Y intercept | Region |
| 5x + y ≥ 10 | 5x + y = 10 | ( ___, 0) | (0, 10) | Away from origin |
| x + y ≥ 6 | x + y = 6 | (6, 0) | (0, ___ ) | Away from origin |
| x + 4y ≥ 12 | x + 4y = 12 | (12, 0) | (0, 3) | Away from origin |
| x, y ≥ 0 | x = 0, y = 0 | x = 0 | y = 0 | 1st quadrant |
∵ Origin has not satisfied the inequations.
∴ Solution of the inequations is away from origin.
The feasible region is unbounded area which is satisfied by all constraints.
In the figure, ABCD represents
The set of the feasible solution where
A(12, 0), B( ___, ___ ), C ( ___, ___ ) and D(0, 10).
The coordinates of B are obtained by solving equations
x + 4y = 12 and x + y = 6
The coordinates of C are obtained by solving equations
5x + y = 10 and x + y = 6
Hence the optimum solution lies at the extreme points.
The optimal solution is in the following table:
| Point | Coordinates | Z = 4x + 5y | Values | Remark |
| A | (12, 0) | 4(12) + 5(0) | 48 | |
| B | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | ______ |
| C | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | |
| D | (0, 10) | 4(0) + 5(10) | 50 |
∴ Z is minimum at ___ ( ___, ___ ) with the value ___
If z = 200x + 500y .....(i)
Subject to the constraints:
x + 2y ≥ 10 .......(ii)
3x + 4y ≤ 24 ......(iii)
x, 0, y ≥ 0 ......(iv)
At which point minimum value of Z is attained.
