Advertisements
Advertisements
प्रश्न
A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system?
उत्तर १
The speed of the centre of mass (CM) of a trolley and child system remains unchanged when the child runs around on a moving trolley with uniform speed V on a smooth floor. This is because the child's movements are internal actions within the trolley-child system, and internal forces do not affect the system's total momentum. With no external forces acting on the system, the CM's velocity remains constant at V.
उत्तर २
The trolley is moving on a smooth horizontal floor, the smoothness of the floor means that no external horizontal forces are acting on the system. When the child runs on the trolley, the forces exerted by the child on the trolley and by the trolley on the child are both internal forces.
`vec"F"_"ext" = vec0`
According to the law of conservation of momentum,
`"M" vec"v"_"cm" = "constant"`;
`vec"v"_"cm" = "constant"`
This implies that the velocity of the center of mass will remain constant.
APPEARS IN
संबंधित प्रश्न
A collision experiment is done on a horizontal table kept in an elevator. Do you expect a change in the result if the elevator is accelerated up or down because of the noninertial character of the frame?
A circular plate of diameter d is kept in contact with a square plate of edge d as show in figure. The density of the material and the thickness are same everywhere. The centre of mass of the composite system will be 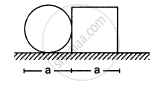
Consider a system of two identical particles. One of the particles is at rest and the other has an acceleration a. The centre of mass has an Acceleration
A ball kept in a closed box moves in the box making collisions with the walls. The box is kept on a smooth surface. The velocity of the centre of mass
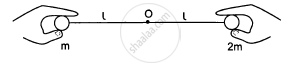
Two balls having masses m and 2m are fastened to two light strings of same length l (See figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a) Find the velocity of the balls just after their collision. (b) How high will the ball rise after the collision?
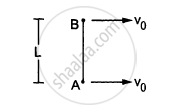
Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (see the following figure). The system translates on a frictionless horizontal surface with a velocity \[\nu_0\] in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the centre of mass C of the system A + B + P and (c) the angular speed of the system about C after the collision.
[Hint : The light rod will exert a force on the ball B
only along its length.]
The centre of mass of a system of two particles divides the distance between them ______.
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
- Show pi = p’i + miV Where pi is the momentum of the ith particle (of mass mi) and p′ i = mi v′ i. Note v′ i is the velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass `sum"p""'"_"t" = 0`
-
Show K = K′ + 1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the
system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the
kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the
system). The result has been used in Sec. 7.14. - Show where `"L""'" = sum"r""'"_"t" xx "p""'"_"t"` is the angular momentum of the system about the centre of mass with
velocities taken relative to the centre of mass. Remember `"r"_"t" = "r"_"t" - "R"`; rest of the notation is the standard notation used in the chapter. Note L′ and MR × V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. - Show `"dL"^"'"/"dt" = ∑"r"_"i"^"'" xx "dP"^"'"/"dt"`
Further show that `"dL"^'/"dt" = τ_"ext"^"'"`
Where `"τ"_"ext"^"'"` is the sum of all external torques acting on the system about the centre of mass.
(Hint: Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Figure).
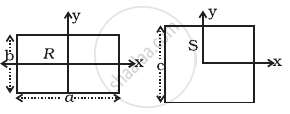
Show that
- IxR/IxS < 1
- IyR/IyS > 1
- IzR/IzS > 1
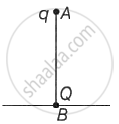
A point charge Q is situated at point B on the ground. A point charge q of mass m is vertically dropped along line AB from a multi-storey building of height h. Find the position of the point charge q when it is in equilibrium.