Advertisements
Advertisements
प्रश्न
A current-carrying circular coil of 100 turns and radius 5.0 cm produces a magnetic field of 6.0 × 10−5 T at its centre. Find the value of the current.
उत्तर
Given:
No. of turns, n = 100
Radius of the loop, r = 5 cm = 0.05 m
Magnetic field intensity, B = 6.0 × 10−5 T
Now, let the magnitude of current be i.
\[\text{ Using } B = \frac{\mu_0 \text{ ni} }{2r}, \text{ we get } \]
\[6 . 0 \times {10}^{- 7} = \frac{4\pi \times {10}^{- 7} \times {10}^2 \times i}{2 \times 0 . 05}\]
\[ \Rightarrow i = \frac{60 \times {10}^{- 7}}{4\pi \times {10}^{- 7} \times {10}^2}\]
\[ = 4 . 777 \times {10}^{- 2} \approx 48\] mA
APPEARS IN
संबंधित प्रश्न
Write the expression for the magnetic moment `vecm`due to a planar square loop of side ‘l’ carrying a steady current I in a vector form.
In the given figure this loop is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance l as shown. Give reason to explain that the loop will experience a net force but no torque. Write the expression for this force acting on the loop.

Is it possible for a current loop to stay without rotating in a uniform magnetic field? If yes, what should be the orientation of the loop?
The torque on a current loop is zero if the angle between the positive normal and the magnetic field is either θ = 0 or θ = 180°. In which of the two orientations, the equilibrium is stable?
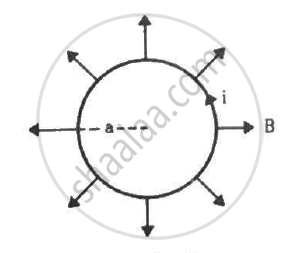
A circular loop of radius a, carrying a current i, is placed in a two-dimensional magnetic field. The centre of the loop coincides with the centre of the field (figure). The strength of the magnetic field at the periphery of the loop is B. Find the magnetic force on the wire.
A current loop of arbitrary shape lies in a uniform magnetic field B. Show that the net magnetic force acting on the loop is zero.
A 50-turn circular coil of radius 2.0 cm carrying a current of 5.0 A is rotated in a magnetic field of strength 0.20 T. (a) What is the maximum torque that acts on the coil? (b) In a particular position of the coil, the torque acting on it is half of this maximum. What is the angle between the magnetic field and the plane of the coil?
A moving coil galvanometer has been fitted with a rectangular coil having 50 turns and dimensions 5 cm × 3 cm. The radial magnetic field in which the coil is suspended is of 0.05 Wb/m2. The torsional constant of the spring is 1.5 × 10−9 Nm/degree. Obtain the current required to be passed through the galvanometer so as to produce a deflection of 30°.
A Rectangular coil of 10 turns, each of area 0.05 m2, is suspended freely in a uniform magnetic field of induction 0.01 T. A current of 30 µA is passed through it.
(i) What is the magnetic moment of the coil?
(ii) What is the maximum torque experienced by the coil?
A 100 turn rectangular coil measuring 0.02 m x 0.06 m of an ammeter is in a magnetic field of induction 0.4 tesla. The torsional constant of the suspension fibre is 5 x 10-7 newton x metre/degree. The maximum reading of the ammeter corresponds to a deflection of the coil through 30°. If the magnetic field is radial, then the maximum current that can be measured with this ammeter is ____________.
The `(tau - theta)` graph for a coil is
A rectangular coil has 200 turns each of area 50 cm2 . It is capable of rotation about an axis joining the mid points of two opposite sides. When a current of 10 A is passed through it while its plane is at right angles to a uniform magnetic field, it experiences a torque of 5 Nm. The magnetic field will be ____________.
The magnetic field developed due to current carrying coil at its centre is 'B'. If the new coil of two turns is prepared from the above coil and same current is passed, then the magnetic field at the centre of the new coil will be ____________.
A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the
(a) total torque on the coil,
(b) total force on the coil,
(c) average force on each electron in the coil due to the magnetic field?
(The coil is made of copper wire of cross-sectional area 10–5 m2, and the free electron density in copper is given to be about 1029 m–3.)
When the plane of the coil is parallel to the field, torque will be ______
A current of 10 A is flowing in a wire of length 1.5 m. A force of 15 N acts on it when it is placed in a uniform magnetic field of 2 T. The angle between the magnetic field and the direction of the current is ______.
Equal current i flows in two segments of a circular loop in the direction shown in figure. Radius of the loop is r. The magnitude of magnetic field induction at the centre of the loop is ______.
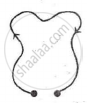
A thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is ______.

Calculate the orbital magnetic dipole moment of the electron in the second Bohr orbit of the hydrogen atom, given the radius of the orbit is 2.1 Å and the orbital speed is 1.1 × 106 m/s.
An electron moving along positive X axis with a velocity of 8 ×107ms-1 enters a region having uniform magnetic field B = 1.3 × 10-3 T along positive Y axis.
- Explain why the electron describes a circular path.
- Calculate the radius of the circular path described by the electron.
