Advertisements
Advertisements
प्रश्न
A 50-turn circular coil of radius 2.0 cm carrying a current of 5.0 A is rotated in a magnetic field of strength 0.20 T. (a) What is the maximum torque that acts on the coil? (b) In a particular position of the coil, the torque acting on it is half of this maximum. What is the angle between the magnetic field and the plane of the coil?
उत्तर
Given:
No. of turns of the coil, n = 50
Magnetic field intensity, B = 0.20 T = 2 × 10−1 T
Radius of the coil, r = 0.02 m = 2 × 10−2 m
Magnitude of current =5 A
Torque acting on the coil,
τ = niABsinθ
Here, A is the area of the coil and θ is the angle between the area vector and the magnetic field.
τ is maximum when θ = 90°.
τmax = niABsin90°
= 50 × 5 × 3.14 × 4 × 10−4 × 2 × 10−1
= 6.28 × 10−2 N-m
Given , ` tau = 1/2 xx tau_max`
⇒ `sintheta = 1/2`
⇒ θ = 30°
So, the angle between the magnetic field and the plane of the coil = 90° − 30° = 60°
APPEARS IN
संबंधित प्रश्न
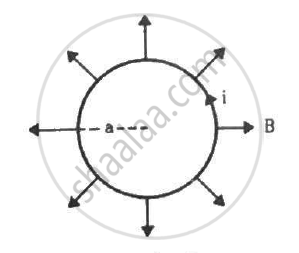
A circular loop of radius a, carrying a current i, is placed in a two-dimensional magnetic field. The centre of the loop coincides with the centre of the field (figure). The strength of the magnetic field at the periphery of the loop is B. Find the magnetic force on the wire.
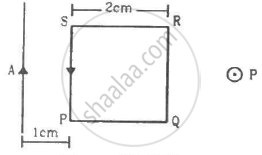
A square loop PQRS carrying a current of 6.0 A is placed near a long wire carrying 10 A as shown in figure. (a) Show that the magnetic force acting on the part PQ is equal and opposite to the part RS. (b) Find the magnetic force on the square loop.
A circular loop of one turn carries a current of 5.00 A. If the magnetic field B at the centre is 0.200 mT, find the radius of the loop.
A current-carrying circular coil of 100 turns and radius 5.0 cm produces a magnetic field of 6.0 × 10−5 T at its centre. Find the value of the current.
Derive the expression for the torque acting on a current-carrying loop placed in a magnetic field.
A moving coil galvanometer has been fitted with a rectangular coil having 50 turns and dimensions 5 cm × 3 cm. The radial magnetic field in which the coil is suspended is of 0.05 Wb/m2. The torsional constant of the spring is 1.5 × 10−9 Nm/degree. Obtain the current required to be passed through the galvanometer so as to produce a deflection of 30°.
Torque acting on a rectangular coil carrying current 'l' situated parallel to magnetic field of induction 'B', having number of turns 'n' and area 'A' is ______.
A 100 turn rectangular coil measuring 0.02 m x 0.06 m of an ammeter is in a magnetic field of induction 0.4 tesla. The torsional constant of the suspension fibre is 5 x 10-7 newton x metre/degree. The maximum reading of the ammeter corresponds to a deflection of the coil through 30°. If the magnetic field is radial, then the maximum current that can be measured with this ammeter is ____________.
The `(tau - theta)` graph for a coil is
If in a moving coil galvanometer, a current I produces a deflection `theta,` then ____________.
Two galvanometers 'G1' and 'G2' require 2 mA and 3 mA respectively to produce the same deflection. Then _______.
If the net magnetic force acting on a loop is zero then ____________.
Which one of the following statements is 'NOT' TRUE? Sensitivity of a moving coil galvanometer can be increased by ____________.
In suspended type of moving coil galvanometer ____________.
A uniform conducting wire of length 12a and resistance R is wound up as a current-carrying coil in the shape of (i) an equilateral triangle of side a; (ii) a square of sides a and, (iii) a regular hexagon of sides a. The coil is connected to a voltage source V0. Find the magnetic moment of the coils in each case.
The initial pressure and volume of a gas enclosed in a cylinder are 2 × 105 N/m2 and 6 × 10-3 m3 respectively. If the work done in compressing the gas at constant pressure is 150 J. find the final volume of the gas.
An electron moving along positive X axis with a velocity of 8 ×107ms-1 enters a region having uniform magnetic field B = 1.3 × 10-3 T along positive Y axis.
- Explain why the electron describes a circular path.
- Calculate the radius of the circular path described by the electron.
