Advertisements
Advertisements
प्रश्न
A rectangular loop of sides 20 cm and 10 cm carries a current of 5.0 A. A uniform magnetic field of magnitude 0.20 T exists parallel to the longer side of the loop. (a) What is the force acting on the loop? (b) What is the torque acting on the loop?
उत्तर
Let ABCD be the rectangular loop.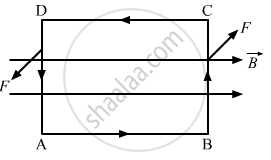
Given:
No. of turns of the coil, n = 50
Magnetic field intensity, B = 0.20 T = 2 × 10−1 T
Magnitude of current, I = 5 A
Length of the loop, l = 20 cm = 20 × 10−2 m,
Breadth of the loop, w = 10 cm = 10 × 10−2 m,
So, area of the loop, A = lw = 0.02 m2,
fig
(a) There is no force on the sides ab and cd, as they are along the magnetic field.
But the force on the sides ad and bc are equal and opposite; so, they cancel each other.
Hence, the net force on the loop is zero.
(b) Torque acting on the coil,
τ = niABsinθ
Here, A is the area of the coil and θ is the angle between the area vector and magnetic field.
τ = niABsin90°
= 1 × 5 × 0.02 × 0.2
= 0.02 N-m
So, the torque acting on the loop is 0.02 N-m and is parallel to the shorter side.
APPEARS IN
संबंधित प्रश्न
Will a current loop placed in a magnetic field always experience a zero force?
The torque on a current loop is zero if the angle between the positive normal and the magnetic field is either θ = 0 or θ = 180°. In which of the two orientations, the equilibrium is stable?
A current loop of arbitrary shape lies in a uniform magnetic field B. Show that the net magnetic force acting on the loop is zero.
A circular loop of one turn carries a current of 5.00 A. If the magnetic field B at the centre is 0.200 mT, find the radius of the loop.
A current-carrying circular coil of 100 turns and radius 5.0 cm produces a magnetic field of 6.0 × 10−5 T at its centre. Find the value of the current.
Derive an expression for the net torque on a rectangular current carrying loop placed in a uniform magnetic field with its rotational axis perpendicular to the field.
Derive the expression for the torque on a current-carrying coil in a magnetic field.
The `(tau - theta)` graph for a coil is
If number of turns in moving coil galvanometer becomes half, then the deflection for the same current will become ____________.
The current flowing through moving coil galvanometer is 20% of the current to be measured. The resistance of moving coil galvanometer is 48 `Omega`, then shunt required is ____________.
The sensitivity of moving coil galvanometer is inversely proportional to ____________.
What is the magnetic moment of a current-carrying circular coil if the radius of the circular coil is 'R' and magnetic induction at the center is 'B'?
Two cylinders A and B of the same material have same length, their radii being in the ratio 1 : 2 respectively. The two are joined end to end as shown in the figure. One end of cylinder A is rigidly clamped while free end of cylinder B is twisted through an angle θ. The angle of twist of cylinder A is ______.
A circular coil having N turns and radius r carries a current I. It is held in the XZ plane in a magnetic field `Bhati`. The torque on the coil due to the magnetic field is ______.
Equal current i flows in two segments of a circular loop in the direction shown in figure. Radius of the loop is r. The magnitude of magnetic field induction at the centre of the loop is ______.
A thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is ______.


Calculate the orbital magnetic dipole moment of the electron in the second Bohr orbit of the hydrogen atom, given the radius of the orbit is 2.1 Å and the orbital speed is 1.1 × 106 m/s.
A circular coil having N turns of radius R carrying a current I is used to produce a magnetic field B at its centre O.
If this coil is opened and rewound such that the radius of the newly formed coil is 2R, carrying the same current I, what will be the magnetic field at the centre O?
