Advertisements
Advertisements
प्रश्न
A 50-turn circular coil of radius 2.0 cm carrying a current of 5.0 A is rotated in a magnetic field of strength 0.20 T. (a) What is the maximum torque that acts on the coil? (b) In a particular position of the coil, the torque acting on it is half of this maximum. What is the angle between the magnetic field and the plane of the coil?
उत्तर
Given:
No. of turns of the coil, n = 50
Magnetic field intensity, B = 0.20 T = 2 × 10−1 T
Radius of the coil, r = 0.02 m = 2 × 10−2 m
Magnitude of current =5 A
Torque acting on the coil,
τ = niABsinθ
Here, A is the area of the coil and θ is the angle between the area vector and the magnetic field.
τ is maximum when θ = 90°.
τmax = niABsin90°
= 50 × 5 × 3.14 × 4 × 10−4 × 2 × 10−1
= 6.28 × 10−2 N-m
Given , ` tau = 1/2 xx tau_max`
⇒ `sintheta = 1/2`
⇒ θ = 30°
So, the angle between the magnetic field and the plane of the coil = 90° − 30° = 60°
APPEARS IN
संबंधित प्रश्न
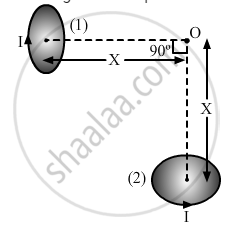
Two very small identical circular loops, (1) and (2), carrying equal currents I are placed vertically (with respect to the plane of the paper) with their geometrical axes perpendicular to each other as shown in the figure. Find the magnitude and direction of the net magnetic field produced at the point O.
Two identical circular loops, P and Q, each of radius r and carrying equal currents are
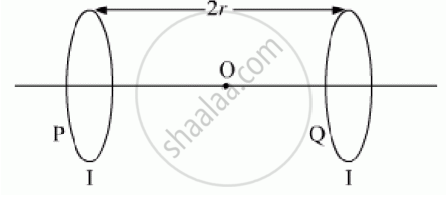
kept in the parallel planes having a common axis passing through O. The direction of current in P is clockwise and in Q is anti-clockwise as seen from O which is equidistant from the loops P and Q. Find the magnitude of the net magnetic field at O.
Will a current loop placed in a magnetic field always experience a zero force?
A circular loop of area 1 cm2, carrying a current of 10 A, is placed in a magnetic field of 0.1 T perpendicular to the plane of the loop. The torque on the loop due to the magnetic field is
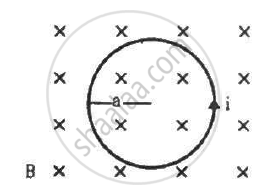
A circular loop of radius a, carrying a current i, is placed in a two-dimensional magnetic field. The centre of the loop coincides with the centre of the field (figure). The strength of the magnetic field at the periphery of the loop is B. Find the magnetic force on the wire.
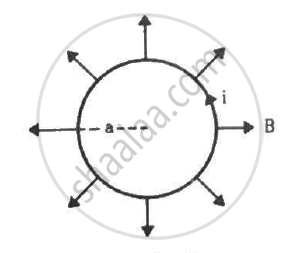
The figure shows a circular wire loop of radius a and carrying a current i, which is placed in a perpendicular magnetic field B. (a) Consider a small part dl of the wire. Find the force on this part of the wire exerted by the magnetic field. (b) Find the force of compression in the wire.
Suppose that the radius of cross-section of the wire used in the previous problem is r. Find the increase in the radius of the loop if the magnetic field is switched off. Young's modulus of the material of the wire is Y.
A current-carrying circular coil of 100 turns and radius 5.0 cm produces a magnetic field of 6.0 × 10−5 T at its centre. Find the value of the current.
A moving coil galvanometer has been fitted with a rectangular coil having 50 turns and dimensions 5 cm × 3 cm. The radial magnetic field in which the coil is suspended is of 0.05 Wb/m2. The torsional constant of the spring is 1.5 × 10−9 Nm/degree. Obtain the current required to be passed through the galvanometer so as to produce a deflection of 30°.
A Rectangular coil of 10 turns, each of area 0.05 m2, is suspended freely in a uniform magnetic field of induction 0.01 T. A current of 30 µA is passed through it.
(i) What is the magnetic moment of the coil?
(ii) What is the maximum torque experienced by the coil?
A triangular loop of side `l` carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is ____________.
If number of turns in moving coil galvanometer becomes half, then the deflection for the same current will become ____________.
The sensitivity of moving coil galvanometer is inversely proportional to ____________.
The magnetic field developed due to current carrying coil at its centre is 'B'. If the new coil of two turns is prepared from the above coil and same current is passed, then the magnetic field at the centre of the new coil will be ____________.
A rectangular coil of 10 turns, each of area 0.05 m2, is suspended freely in a radial magnetic field of 0.01 T. If the torsional constant of the suspension fibre is 5 × 10−9 N·m per degree, find the angle through which the coil rotates when a current of 30 μA is passed through it.
Write the formula for torque acting on rotating current carrying coil in terms of magnetic dipole moment, in vector form.
A circular coil having N turns of radius R carrying a current I is used to produce a magnetic field B at its centre O.
If this coil is opened and rewound such that the radius of the newly formed coil is 2R, carrying the same current I, what will be the magnetic field at the centre O?
An electron moving along positive X axis with a velocity of 8 ×107ms-1 enters a region having uniform magnetic field B = 1.3 × 10-3 T along positive Y axis.
- Explain why the electron describes a circular path.
- Calculate the radius of the circular path described by the electron.
