Advertisements
Advertisements
प्रश्न
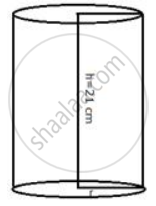
A cylinder of circumference 8 cm and length 21 cm rolls without sliding for `4 1/2` seconds at the rate of 9 complete rounds per second. Find the distance travelled by the cylinder in `4 1/2` seconds.
उत्तर
Circumference of cylinder = 8 cm
Therefore, radius = `c/(2pi) = (8 xx 7)/(2 xx 22) = 14/11 cm`
Length of the cylinder (h) = 21 cm
If distance covered in one revolution is 8 cm, then distance covered in 9 revolution = 9 × 8 = 72
Therefore, distance covered in `4 1/2` seconds
= `72 xx 9/2 cm`
= 324 cm
APPEARS IN
संबंधित प्रश्न
The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm3 of wood has a mass of 0.6 g.
`["Assume "pi=22/7]`
A hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into conical shaped small container each of diameter 3 cm and height 4 cm. How many container are necessary to empty the bowl?
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 80 m, calculate the total area of canvas required. Also, find the total cost of canvas used at Rs. 15 per metre if the width is 1.5 m.
A metal pipe has a bore (inner diameter) of 5 cm. The pipe is 5 mm thick all round. Find the weight, in kilogram, of 2 metres of the pipe if 1 cm3 of the metal weights 7.7 g.
Two right circular solid cylinders have radii in the ratio 3 : 5 and heights in the ratio 2 : 3. Find the ratio between their curved surface areas.
A 14 m deep well with inner diameter 10 m is dug and the earth taken out is evenly spread all around the well to form an embankment of width 5 m. Find the height of the embankment.
If the radius of a cylinder is doubled and height is halved, the volume will be doubled.
Radius of a cylinder is r and the height is h. Find the change in the volume if the height is doubled and the radius is halved.
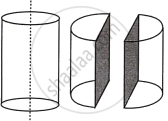
A solid metallic cylinder is cut into two identical halves along its height (as shown in the diagram). The diameter of the cylinder is 7 cm and the height is 10 cm.
Find:
- The total surface area (both the halves).
- The total cost of painting the two halves at the rate of ₹ 30 per cm2 `("Use" π = 22/7)`.