Advertisements
Advertisements
Question
A cylinder of circumference 8 cm and length 21 cm rolls without sliding for `4 1/2` seconds at the rate of 9 complete rounds per second. Find the distance travelled by the cylinder in `4 1/2` seconds.
Solution
Circumference of cylinder = 8 cm
Therefore, radius = `c/(2pi) = (8 xx 7)/(2 xx 22) = 14/11 cm`
Length of the cylinder (h) = 21 cm
If distance covered in one revolution is 8 cm, then distance covered in 9 revolution = 9 × 8 = 72
Therefore, distance covered in `4 1/2` seconds
= `72 xx 9/2 cm`
= 324 cm
APPEARS IN
RELATED QUESTIONS
If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, then find (i) radius of its base (ii) its volume. [Use π = 3.14]
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and same base is removed. Find the volume of the remaining solid.
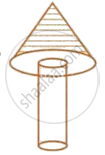
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside. If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm; find the total surface area of the toy. [Take π = 3.14]
A cylindrical container with diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 22 cm × 14 cm × 10.5 cm. Find the rise in the level of the water when the solid is submerged.
How many cubic meters of earth must be dug out to make a well 28 m deep and 2.8 m in diameter ? Also, find the cost of plastering its inner surface at Rs 4.50 per sq meter.
A cylindrical container with internal radius of its base 10 cm, contains water up to a height of 7 cm. Find the area of the wet surface of the cylinder.
The height and the radius of the base of a cylinder are in the ratio 3 : 1. If it volume is 1029 π cm3; find it total surface area.
Find the volume of the largest cylinder formed when a rectangular piece of paper 44 cm by 33 cm is rolled along its :
- shorter side.
- longer side.
A glass cylinder with a diameter 20 cm has water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which the water will up in the cylinder. Answer correct of the nearest mm. (Take π = 3.142)
Radius of a cylinder is r and the height is h. Find the change in the volume if the height is doubled.
