Advertisements
Advertisements
प्रश्न
A cylindrical vessel of height 24 cm and diameter 40 cm is full of water. Find the exact number of small cylindrical bottles, each of height 10 cm and diameter 8 cm, which can be filled with this water.
उत्तर
For a large cylindrical vessel,
Height = H = 24 cm
Radius = R = `40/2` = 20 cm
∴ Volume of large cylindrical vessel = πR2H
= (π × 20 × 20 × 24) cm3
For each small cylindrical bottle,
Height = h = 10 cm
Radius = r = `8/2` = 4 cm
∴ Volume of each small cylindrical bottle = πr2h
= (π × 4 × 4 × 10) cm3
Now, number of small cylindrical bottles which can filled
= `"Volume of large cylindrival vessel"/"Volume of each small cylindrical bottle"`
= `(pi xx 20 xx 20 xx 24)/(pi xx 4 xx 4 xx 10)`
= 60
APPEARS IN
संबंधित प्रश्न
A cylindrical can, whose base is horizontal and of radius 3.5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate:
- the total surface area of the can in contact with water when the sphere is in it;
- the depth of water in the can before the sphere was put into the can.
Water flows, at 9 km per hour, through a cylindrical pipe of cross-sectional area 25 cm2. If this water is collected into a rectangular cistern of dimensions 7.5 m by 5 m by 4 m; calculate the rise in level in the cistern in 1 hour 15 minutes.
An exhibition tent is in the form of a cylinder surmounted by a cone. The height of the tent above the ground is 85 m and height of the cylindrical part of 50 m. If the diameter of the base is 168 m, find the quantity of canvas required to make the tent. Allow 20% extra for fold and for stitching. Give your answer to the nearest m2.
A cylinder of circumference 8 cm and length 21 cm rolls without sliding for `4 1/2` seconds at the rate of 9 complete rounds per second. Find the distance travelled by the cylinder in `4 1/2` seconds.
How much water will a tank hold if the interior diameter of the tank is 1.6 m and its depth is 0.7 m?
The height of a circular cylinder is 20 cm and the radius of its base is 7 cm. Find : the total surface area.
In a hollow cylinder, the sum of the external and internal radii is 14 cm and the width is 4 cm. If its height is 20 cm, the volume of the material in it is
30 circular plates, each of radius 14 cm and thickness 3 cm are placed one above the another to form a cylindrical solid. Find volume of the cylinder so formed.
A housing society consisting of 5,500 people needs 100 L of water per person per day. The cylindrical supply tank is 7 m high and has a diameter 10 m. For how many days will the water in the tank last for the society?
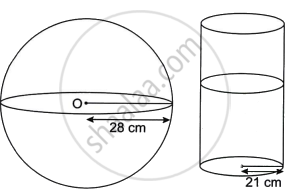
Oil is stored in a spherical vessel occupying `3/4` of its full capacity. Radius of this spherical vessel is 28 cm. This oil is then poured into a cylindrical vessel with a radius of 21 cm. Find the height of the oil in the cylindrical vessel (correct to the nearest cm). Take π = `22/7`