Advertisements
Advertisements
प्रश्न
A lawn is in the shape of a semicircle of diameter 42m. the lawn is surrounded by a flower bed of width 7m all round. Find the area of the flower bed in m2.
उत्तर

There are two concentric semi circles. The diameter of the inner circle = 42 or radius, a = 21m. The radius of the outer circle, b = 21 + 7 = 28m.
Because the radius of a Circle with diameter d is r = `"d"/(2)`
The Area of the inner Semi-circle with radius a = `(pi"a"^2)/(2) = (pi21^2)/(2)`
∴ The Area of the outer Semi-circle with radius b = `(pi"b"^2)/(2) = (pi28^2)/(2)`
and The Area of a Semi-circle with radius r = `(pi"r"^2)/(2)`
The Area of the flower bed
= `(pi28^2)/(2) - (pi21^2)/(2)`
= `pi/(2)(28^2 - 21^2)`
= `pi/(2)(784 - 441)`
= `pi/(2)(343)`
= `(22)/(7 xx 2)(343)`
= 539m2.
APPEARS IN
संबंधित प्रश्न
Find the length of the diagonal of a square whose area is `128 cm^2` Also, find its perimeter.
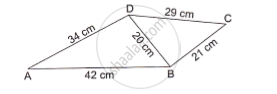
Find the area of the quadrilateral ABCD in which in AB=42 cm, BC=21 cm, CD=29cm, DA=34 cm and diagonal BD = 20 cm.
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of the sector of the circle formed by chord AB.
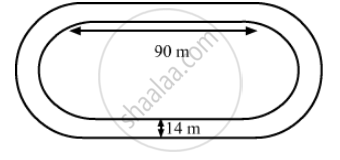
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

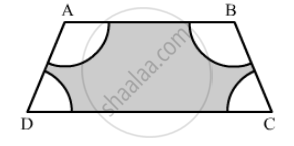
In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm DC = 32 cm and the distance between AB and DC is 14 cm. Circles of equal radii 7 cm with centres A, B, C and D have been drawn. Then find the area of the shaded region.
(Use \[\pi = \frac{22}{7}\]
An arc subtends an angle of 90° at the centre of the circle of the radius 14 cm. Write the area of minor sector thus formed in terms of π.
The circumference of a circle is 100 m. The side of a square inscribed in the circle is
If the area of a sector of a circle is `5/18` of the area of the circle, then the sector angle is equal to
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of radii 40cm and 9cm?
