Advertisements
Advertisements
प्रश्न
A man, 2m tall, walks at the rate of `1 2/3` m/s towards a street light which is `5 1/3`m above the ground. At what rate is the tip of his shadow moving? At what rate is the length of the shadow changing when he is `3 1/3`m from the base of the light?
उत्तर
Let AB is the height of street light post and CD is the height of the man such that
AB = `5 1/3 = 16/3 "m"` and CD = 2 m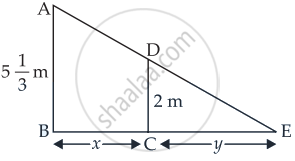
Let BC = x length (the distance of the man from the lamp post) and CE = y is the length of the shadow of the man at any instant.
From the figure, we see that
ΔABE ~ Δ DCE ......[By AAA Similarity]
∴ Taking ratio of their corresponding sides, we get
`"AB"/"CD" = "BE"/"CE"`
⇒ `"AB"/"CD" = ("BC" + "CE")/"CE"`
⇒ `(16/3)/2 = (x + y)/y`
⇒ `8/3 = (x + y)/y`
⇒ 8y = 3x + 3y
⇒ 8y – 3y = 3x
⇒ 5y = 3x
Differentiating both sides w.r.t, t, we get
`"dy"/"dt" = 3 * "dx"/dt"`
⇒ `"dy"/"dt" = 3/5 * "dx"/"dt"`
⇒ `"dy"/"dt" = 3/5 * ((-5)/3)` ......[∵ man is moving in opposite direction]
= – 1 m/s
Hence, the length of shadow is decreasing at the rate of 1 m/s.
Now let u = x + y .....(u = Distance of the tip of shadow from the light post)
Differentiating both sides w.r.t. t, we get
`"du"/"dt" = "dx"/"dt" + "dy"/dt"`
= `(- 1 2/3 - 1)`
= `-(5/3 + 1)`
= `- 8/3`
= `-2 2/3` m/s
Hence, the tip of the shadow is moving at the rate of `2 2/3` m/s towards the light post and the length of shadow decreasing at the rate of 1 m/s.
APPEARS IN
संबंधित प्रश्न
The rate of change of the area of a circle with respect to its radius r at r = 6 cm is ______.
The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base?
The sum of the perimeter of a circle and square is k, where k is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.
The total cost C (x) associated with the production of x units of an item is given by C (x) = 0.007x3 − 0.003x2 + 15x + 4000. Find the marginal cost when 17 units are produced ?
The total revenue received from the sale of x units of a product is given by R (x) = 13x2 + 26x + 15. Find the marginal revenue when x = 7 ?
The radius of a spherical soap bubble is increasing at the rate of 0.2 cm/sec. Find the rate of increase of its surface area, when the radius is 7 cm.
A particle moves along the curve y = x2 + 2x. At what point(s) on the curve are the x and y coordinates of the particle changing at the same rate?
A particle moves along the curve y = x3. Find the points on the curve at which the y-coordinate changes three times more rapidly than the x-coordinate.
A man 2 metres high walks at a uniform speed of 6 km/h away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases ?
The radius of a cylinder is increasing at the rate 2 cm/sec. and its altitude is decreasing at the rate of 3 cm/sec. Find the rate of change of volume when radius is 3 cm and altitude 5 cm.
A particle moves along the curve y = (2/3)x3 + 1. Find the points on the curve at which the y-coordinate is changing twice as fast as the x-coordinate ?
Find the point on the curve y2 = 8x for which the abscissa and ordinate change at the same rate ?
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of the perimeter.
The side of a square is increasing at the rate of 0.1 cm/sec. Find the rate of increase of its perimeter ?
A cone whose height is always equal to its diameter is increasing in volume at the rate of 40 cm3/sec. At what rate is the radius increasing when its circular base area is 1 m2?
The volume of a sphere is increasing at the rate of 4π cm3/sec. The rate of increase of the radius when the volume is 288 π cm3, is
If s = t3 − 4t2 + 5 describes the motion of a particle, then its velocity when the acceleration vanishes, is
A man 2 metres tall walks away from a lamp post 5 metres height at the rate of 4.8 km/hr. The rate of increase of the length of his shadow is
A man of height 6 ft walks at a uniform speed of 9 ft/sec from a lamp fixed at 15 ft height. The length of his shadow is increasing at the rate of
The rate of change of volume of a sphere with respect to its surface area, when the radius is 2 cm, is ______.
A spherical ball of salt is dissolving in water in such a manner that the rate of decrease of the volume at any instant is proportional to the surface. Prove that the radius is decreasing at a constant rate
A kite is moving horizontally at a height of 151.5 meters. If the speed of kite is 10 m/s, how fast is the string being let out; when the kite is 250 m away from the boy who is flying the kite? The height of boy is 1.5 m.
A swimming pool is to be drained for cleaning. If L represents the number of litres of water in the pool t seconds after the pool has been plugged off to drain and L = 200 (10 – t)2. How fast is the water running out at the end of 5 seconds? What is the average rate at which the water flows out during the first 5 seconds?
Total revenue in rupees received from the sale of x units of a product is given by R(x)= 3x2+ 36x + 5. The marginal revenue, when x = 15 is ____________.
The rate of change of volume of a sphere is equal to the rate of change of the radius than its radius equal to ____________.
What is the rate of change of the area of a circle with respect to its radius when, r = 3 cm
If equal sides of an isosceles triangle with fixed base 10 cm are increasing at the rate of 4 cm/sec, how fast is the area of triangle increasing at an instant when all sides become equal?
The median of an equilateral triangle is increasing at the ratio of `2sqrt(3)` cm/s. Find the rate at which its side is increasing.
