Advertisements
Advertisements
प्रश्न
A monkey of mass 40 kg climbs on a rope in given Figure which can stand a maximum tension of 600 N. In which of the following cases will the rope break: the monkey
(a) climbs up with an acceleration of 6 m s–2
(b) climbs down with an acceleration of 4 m s–2
(c) climbs up with a uniform speed of 5 m s–1
(d) falls down the rope nearly freely under gravity?
(Ignore the mass of the rope).
Advertisements
उत्तर १
Case (a)
Mass of the monkey, m = 40 kg
Acceleration due to gravity, g = 10 m/s
Maximum tension that the rope can bear, Tmax = 600 N
Acceleration of the monkey, a = 6 m/s2 upward
Using Newton’s second law of motion, we can write the equation of motion as:
T – mg = ma
∴T = m(g + a)
= 40 (10 + 6)
= 640 N
Since T > Tmax, the rope will break in this case.
Case (b)
Acceleration of the monkey, a = 4 m/s2 downward
Using Newton’s second law of motion, we can write the equation of motion as:
mg – T = ma
∴T = m (g – a)
= 40(10 – 4)
= 240 N
Since T < Tmax, the rope will not break in this case.
Case (c)
The monkey is climbing with a uniform speed of 5 m/s. Therefore, its acceleration is zero, i.e., a = 0.
Using Newton’s second law of motion, we can write the equation of motion as:
T – mg = ma
T – mg = 0
∴T = mg
= 40 × 10
= 400 N
Since T < Tmax, the rope will not break in this case.
Case (d)
When the monkey falls freely under gravity, its will acceleration become equal to the acceleration due to gravity, i.e., a = g
Using Newton’s second law of motion, we can write the equation of motion as:
mg – T = mg
∴T = m(g – g) = 0
Since T < Tmax, the rope will not break in this case.
उत्तर २
(a) When the monkey climbs up with an acceleration a, then T – mg = ma where T represents the tension in figure.
:. T = mg + ma = m (g +a)
or T = 40 kg(10 + 6) ms^(-2) = 640 N
But the rope can withstand a maximum tension of 600 N. So the rope will break
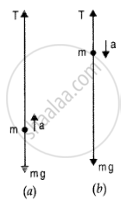
b) When the monkey is climbing down with an acceleration, then
mg - T =ma (Figure b)
=> T = mg - ma = m(g -a)
or T = 40 kg x (10 - 4) `ms^2` = 240 N
(c) When the monkey climbs up with uniform speed, then T mg = 40 kg x 10 ms-2 = 400 N The rope will hot break.
(d) When the monkey is falling freely, it would be a state of weightlessness. So, tension will be zero and the rope will not break.
संबंधित प्रश्न
The rear side of a truck is open and a box of 40 kg mass is placed 5 m away from the open end as shown in Figure. The coefficient of friction between the box and the surface below it is 0.15. On a straight road, the truck starts from rest and accelerates with 2 m s–2. At what distance from the starting point does the box fall off the truck? (Ignore the size of the box).
You are travelling in a car. The driver suddenly applies the brakes and you are pushed forward. Why does this happen?
A spy jumps from an airplane with his parachute. The spy accelerates downward for some time when the parachute opens. The acceleration is suddenly checked and the spy slowly falls to the ground. Explain the action of the parachute in checking the acceleration.
A free 238U nucleus kept in a train emits an alpha particle. When the train is stationary, a nucleus decays and a passenger measures that the separation between the alpha particle and the recoiling nucleus becomes x at time t after the decay. If the decay takes place while the train is moving at a uniform velocity v, the distance between the alpha particle and the recoiling nucleus at a time t after the decay, as measured by the passenger, is
A person is standing on a weighing machine placed on the floor of an elevator. The elevator starts going up with some acceleration, moves with uniform velocity for a while and finally decelerates to stop. The maximum and the minimum weights recorded are 72 kg and 60 kg, respectively. Assuming that the magnitudes of acceleration and deceleration are the same, find (a) the true weight of the person and (b) the magnitude of the acceleration. Take g = 9.9 m/s2.
A constant force F = m2g/2 is applied on the block of mass m1 as shown in the following figure. The string and the pulley are light and the surface of the table is smooth. Find the acceleration of m1.
In the previous problem, suppose m2 = 2.0 kg and m3 = 3.0 kg. What should be the mass m, so that it remains at rest?
Find the mass M of the hanging block in the following figure that will prevent the smaller block from slipping over the triangular block. All the surfaces are frictionless and the strings and the pulleys are light.
Find the acceleration of the 500 g block in the following figure.
In the following figure shows a man of mass 60 kg standing on a light weighing machine kept in a box of mass 30 kg. The box is hanging from a pulley fixed to the ceiling by a light rope, the other end of which is held by the man himself. If the man manages to keep the box at rest, what is the weight recorded on the machine? What force should he exert on the rope to record his correct weight on the machine?
A body of mass m moving with a velocity v is acted upon by a force. Write an expression for change in momentum in each of the following cases: (i) When v << c, (ii) When v → c and (iii) When v << c but m does not remain constant. Here, c is the speed of light.
State two factors which determine the momentum of a body.
State Newton's second law of motion. Is Newton's first law of motion contained in Newton's second law of motion?
Use Newton's second law to explain the following:
We always prefer to land on sand instead of hard floor while taking a high jump.
A ball is thrown vertically downward with an initial velocity of 10 m/s. What is its speed 1 s later and 2 s later?
A stone is dropped from a tower 98 m high. With what speed should a second stone be thrown 1 s later so that both hit the ground at the same time?
Why does a child feel more pain when she falls down on a hard cement floor, than when she falls on the soft muddy ground in the garden?
According to Newton's Second Law of Motion, what quantity is directly proportional to the applied force?
Why is catching a slow-moving ball easier than catching a fast-moving ball?
How does moving your hand backward while catching a cricket ball reduce pain?
