Advertisements
Advertisements
प्रश्न
A monkey of mass 40 kg climbs on a rope in given Figure which can stand a maximum tension of 600 N. In which of the following cases will the rope break: the monkey
(a) climbs up with an acceleration of 6 m s–2
(b) climbs down with an acceleration of 4 m s–2
(c) climbs up with a uniform speed of 5 m s–1
(d) falls down the rope nearly freely under gravity?
(Ignore the mass of the rope).

उत्तर १
Case (a)
Mass of the monkey, m = 40 kg
Acceleration due to gravity, g = 10 m/s
Maximum tension that the rope can bear, Tmax = 600 N
Acceleration of the monkey, a = 6 m/s2 upward
Using Newton’s second law of motion, we can write the equation of motion as:
T – mg = ma
∴T = m(g + a)
= 40 (10 + 6)
= 640 N
Since T > Tmax, the rope will break in this case.
Case (b)
Acceleration of the monkey, a = 4 m/s2 downward
Using Newton’s second law of motion, we can write the equation of motion as:
mg – T = ma
∴T = m (g – a)
= 40(10 – 4)
= 240 N
Since T < Tmax, the rope will not break in this case.
Case (c)
The monkey is climbing with a uniform speed of 5 m/s. Therefore, its acceleration is zero, i.e., a = 0.
Using Newton’s second law of motion, we can write the equation of motion as:
T – mg = ma
T – mg = 0
∴T = mg
= 40 × 10
= 400 N
Since T < Tmax, the rope will not break in this case.
Case (d)
When the monkey falls freely under gravity, its will acceleration become equal to the acceleration due to gravity, i.e., a = g
Using Newton’s second law of motion, we can write the equation of motion as:
mg – T = mg
∴T = m(g – g) = 0
Since T < Tmax, the rope will not break in this case.
उत्तर २
(a) When the monkey climbs up with an acceleration a, then T – mg = ma where T represents the tension in figure.
:. T = mg + ma = m (g +a)
or T = 40 kg(10 + 6) ms^(-2) = 640 N
But the rope can withstand a maximum tension of 600 N. So the rope will break
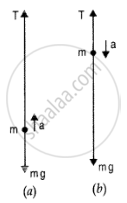
b) When the monkey is climbing down with an acceleration, then
mg - T =ma (Figure b)
=> T = mg - ma = m(g -a)
or T = 40 kg x (10 - 4) `ms^2` = 240 N
(c) When the monkey climbs up with uniform speed, then T mg = 40 kg x 10 ms-2 = 400 N The rope will hot break.
(d) When the monkey is falling freely, it would be a state of weightlessness. So, tension will be zero and the rope will not break.
APPEARS IN
संबंधित प्रश्न
A small block B is placed on another block A of mass 5 kg and length 20 cm. Initially, the block B is near the right end of block A (In the following Figure). A constant horizontal force of 10 N is applied to the block A. All the surfaces are assumed frictionless. Find the time that elapses before block B separates from A.

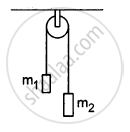
In a simple Atwood machine, two unequal masses m1 and m2 are connected by a string going over a clamped light smooth pulley. In a typical arrangement (In the following figure), m1 = 300 g and m2 = 600 g. The system is released from rest. (a) Find the distance travelled by the first block in the first two seconds; (b) find the tension in the string; (c) find the force exerted by the clamp on the pulley.
In the following figure shows a uniform rod of length 30 cm and mass 3.0 kg. The strings shown in the figure are pulled by constant forces of 20 N and 32 N. Find the force exerted by the 20 cm part of the rod on the 10 cm part. All the surfaces are smooth and the strings and the pulleys are light.

Find the acceleration of the blocks A and B in the three situations shown in the following figure.

Two balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare:
(i) Their inertia.
(ii) Their momentum.
(iii) The force needed to stop them in the same time.
Use Newton's second law of motion to explain the following instance :
A cricketer pulls his hands back while catching a fast moving cricket ball .
An electron of mass 9 × 10−31 kg is moving with a linear velocity of 6 × 107 ms−1. Calculate the linear momentum of electron.
What causes motion in a body?
A ball is thrown upward and reaches a maximum height of 19.6 m. Find its initial speed?
The motion of a particle of mass m is given by x = 0 for t < 0 s, x(t) = A sin 4 pt for 0 < t < (1/4) s (A > o), and x = 0 for t > (1/4) s. Which of the following statements is true?
- The force at t = (1/8) s on the particle is – 16π2 Am.
- The particle is acted upon by on impulse of magnitude 4π2 A m at t = 0 s and t = (1/4) s.
- The particle is not acted upon by any force.
- The particle is not acted upon by a constant force.
- There is no impulse acting on the particle.
