Advertisements
Advertisements
प्रश्न
A rectangular frame is to be suspended symmetrically by two strings of equal length on two supports (Figure). It can be done in one of the following three ways;
| (a) |  |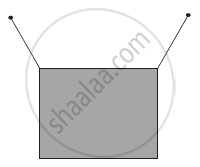
| (b) |  |
| (c) |  |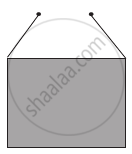
The tension in the strings will be ______.
विकल्प
the same in all cases.
least in (a).
least in (b).
least in (c).
Advertisements
उत्तर
The tension in the strings will be least in (b).
Explanation:
Consider the FBD diagram of the rectangular frame
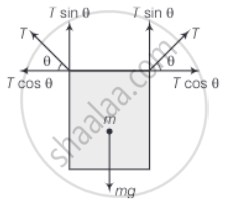
Balancing vertical forces 2T sin θ – mg = 0 ......[T is tension in the string]
⇒ 2T sin θ = mg ......(i)
Total horizontal force = T cos θ – T cos θ = 0
Now from equation (i), T = `(mg)/(2 sin θ)`
As mg is constant
⇒ `T ∝ 1/sin θ`
⇒ `T_(max) = (mg)/(2 sin θ_(min))`
`sin θ_(min)` = 0
⇒ `θ_(min)` = 0
No option matches with θ = 0°
`T_(min) = (mg)/(2 sin θ_(max))` ......(since, sin θmax = 1)
sin θmax = 1
⇒ θ = 90°
Matches with option (b)
Hence, tension is least for case (b).
APPEARS IN
संबंधित प्रश्न
Determine the volume contraction of a solid copper cube, 10 cm on an edge, when subjected to a hydraulic pressure of 7.0 ×106 Pa.
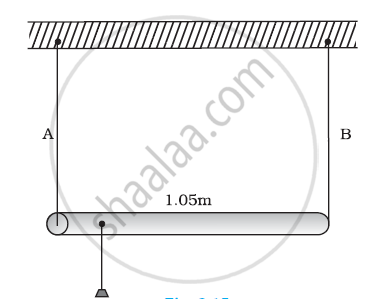
A rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in Figure. The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
A mild steel wire of length 1.0 m and cross-sectional area 0.50 × 10–2 cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the midpoint.
Two strips of metal are riveted together at their ends by four rivets, each of diameter 6.0 mm. What is the maximum tension that can be exerted by the riveted strip if the shearing stress on the rivet is not to exceed 6.9 × 107 Pa? Assume that each rivet is to carry one-quarter of the load.
A steel blade placed gently on the surface of water floats on it. If the same blade is kept well inside the water, it sinks. Explain.
A rope 1 cm in diameter breaks if the tension in it exceeds 500 N. The maximum tension that may be given to a similar rope of diameter 2 cm is
A wire can sustain the weight of 20 kg before breaking. If the wire is cut into two equal parts, each part can sustain a weight of
A heave uniform rod is hanging vertically form a fixed support. It is stretched by its won weight. The diameter of the rod is
When a metal wire is stretched by a load, the fractional change in its volume ∆V/V is proportional to
Answer in one sentence.
How should be a force applied on a body to produce shearing stress?
A spring is stretched by applying a load to its free end. The strain produced in the spring is ______.
A mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pillars (Figure). A mass m is suspended from the mid point of the wire. Strain in the wire is ______.
The value of tension in a long thin metal wire has been changed from T1 to T2. The lengths of the metal wire at two different values of tension T1 and T2 are l1 and l2 respectively. The actual length of the metal wire is ______.
A body of mass m = 10 kg is attached to one end of a wire of length 0.3 m. The maximum angular speed (in rad s-1) with which it can be rotated about its other end in the space station is (Breaking stress of wire = 4.8 × 107 Nm-2 and the area of cross-section of the wire = 10-2 cm2) is ______.
What are the dimensions of stress?
