Advertisements
Advertisements
प्रश्न
A sonometer wire supports a 4 kg load and vibrates in fundamental mode with a tuning fork of frequency 416. Hz. The length of the wire between the bridges is now doubled. In order to maintain fundamental mode, the load should be changed to
विकल्प
1 kg
2 kg
8 kg
16 kg.
उत्तर
16 kg
According to the relation of the fundamental frequency of a string
\[\nu = \frac{1}{2l}\sqrt{\frac{F}{\mu}}\]
where l is the length of the string
F is the tension
μ is the linear mass density of the string
We know that ν1 = 416 Hz, l1 = l and l2 = 2l.
Also, m1 = 4 kg and m2 = ?
\[\nu_1 = \frac{1}{2 l_1}\sqrt{\frac{m_1 g}{\mu}}.................. (1)\]
\[\nu_2 = \frac{1}{2 l_2}\sqrt{\frac{m_2 g}{\mu}} (2)\]
So, in order to maintain the same fundamental mode
\[\nu_1 = \nu_2\]
squaring both sides of equations (1) and (2) and then equating
\[\frac{1}{4 l^2}\frac{4g}{\mu} = \frac{1}{16 l^2}\frac{m_2 g}{\mu}\]
\[ \Rightarrow m_2 = 16 kg\]
APPEARS IN
संबंधित प्रश्न
A stone dropped from the top of a tower of height 300 m high splashes into the water of a pond near the base of the tower. When is the splash heard at the top given that the speed of sound in air is 340 m s–1? (g= 9.8 m s–2)
A hospital uses an ultrasonic scanner to locate tumours in a tissue. What is the wavelength of sound in the tissue in which the speed of sound is 1.7 km s–1? The operating frequency of the scanner is 4.2 MHz.
A SONAR system fixed in a submarine operates at a frequency 40.0 kHz. An enemy submarine moves towards the SONAR with a speed of 360 km h–1. What is the frequency of sound reflected by the submarine? Take the speed of sound in water to be 1450 m s–1.
Show that the particle speed can never be equal to the wave speed in a sine wave if the amplitude is less than wavelength divided by 2π.
A pulse travelling on a string is represented by the function \[y = \frac{a^2}{\left( x - \nu t \right)^2 + a^2},\] where a = 5 mm and ν = 20 cm-1. Sketch the shape of the string at t = 0, 1 s and 2 s. Take x = 0 in the middle of the string.
A wave propagates on a string in the positive x-direction at a velocity \[\nu\] \[t = t_0\] is given by \[g\left( x, t_0 \right) = A \sin \left( x/a \right)\]. Write the wave equation for a general time t.
A wave travelling on a string at a speed of 10 m s−1 causes each particle of the string to oscillate with a time period of 20 ms. (a) What is the wavelength of the wave? (b) If the displacement of a particle of 1⋅5 mm at a certain instant, what will be the displacement of a particle 10 cm away from it at the same instant?
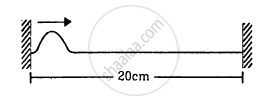
A string of length 20 cm and linear mass density 0⋅40 g cm−1 is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t = 0 near an ends as shown in the figure, which travels towards the other end. (a) When will the string have the shape shown in the figure again? (b) Sketch the shape of the string at a time half of that found in part (a).
A string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160 N m−1 and is stretched by 1⋅0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring?
Following figure shows two wave pulses at t = 0 travelling on a string in opposite directions with the same wave speed 50 cm s−1. Sketch the shape of the string at t = 4 ms, 6 ms, 8 ms, and 12 ms.
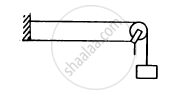
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
An organ pipe of length 0.4 m is open at both ends. The speed of sound in the air is 340 m/s. The fundamental frequency is ______
What is the interference of sound waves?
A string 1 m long is fixed at one end. The other end is moved up and down with a frequency of 20 Hz. Due to this, a stationary wave with four complete loops gets produced on the string. Find the speed of the progressive wave which produces the stationary wave.
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with temperature.
A sound wave is passing through air column in the form of compression and rarefaction. In consecutive compressions and rarefactions ______.
Speed of sound waves in a fluid depends upon ______.
- directty on density of the medium.
- square of Bulk modulus of the medium.
- inversly on the square root of density.
- directly on the square root of bulk modulus of the medium.
At what temperatures (in °C) will the speed of sound in air be 3 times its value at O°C?
Two perfectly identical wires kept under tension are in unison. When the tension in the wire is increased by 1% then on sounding them together 3 beats are heard in 2 seconds. What is the frequency of each wire?
