Advertisements
Advertisements
प्रश्न
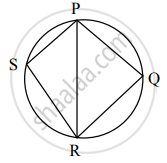
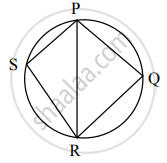
आकृतीमध्ये, `square`PQRS हा चक्रीय चौकोन आहे. बाजू PQ ≅ बाजू RQ, ∠PSR = 110°, तर m(कंस PQR) = किती?
उत्तर
∠PSR = `1/2`m(कंस PQR) ............…[अंतर्लिखित कोनाचे प्रमेय]
∴ 110° = `1/2`m(कंस PQR)
∴ m(कंस PQR) = 220°
APPEARS IN
संबंधित प्रश्न
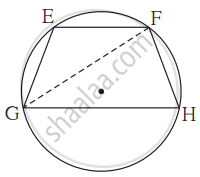
दिलेल्या आकृतीत, जीवा EF || जीवा GH. तर सिद्ध करा, जीवा EG ≅ जीवा FH . पुढे दिलेल्या सिद्धतेतील रिकाम्या जागा भरा आणि सिद्धता लिहा. सिद्धता : रेख GF काढला.
∠EFG = ∠FGH ....... ______ (I)
∠EFG = ______ (अंतर्लिखित कोनाचे प्रमेय) (II)
∠FGH = ______ (अंतर्लिखित कोनाचे प्रमेय) (III)
∴ m (कंस EG) = ______ [(I), (II) व (III) वरून]
जीवा EG ≅ जीवा FH .......(______)
आकृती मध्ये रेषा PR वर्तुळाला बिंदू Q मध्ये स्पर्श करते. या आकृतीच्या आधारे खालील प्रश्नाचं उत्तर लिहा.
∠QTS शी एकरूप असणारे कोन कोणते?
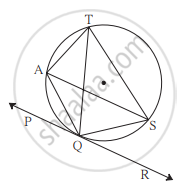
आकृती मध्ये रेषा PR वर्तुळाला बिंदू Q मध्ये स्पर्श करते. या आकृतीच्या आधारे खालील प्रश्नाचं उत्तर लिहा.
जर ∠TAS = 65°, तर ∠TQS आणि कंस TS यांची मापे सांगा.

सिद्ध करा: एकाच कंसात अंतर्लिखित झालेले कोन हे एकरूप असतात.

पक्ष : ∠PQR व ∠PSR एकाच कंसात अंतर्लिखित झालेले कोन आहेत, कंस PTR हा त्या कोनांनी अंतर्खंडित केलेला कंस आहे.
साध्य : ∠PQR ≅ ∠PSR
सिद्धता:
m∠PQR = `1/2 xx` [m(कंस PTR)] .......(i) `square`
m∠`square = 1/2 xx` [mकंस PTR] ........(ii) `square`
m∠`square` = m∠PSR ..................[(i) व (ii) वरून]
∴ ∠PQR ≅ ∠PSR
खालील प्रमेय सिद्ध करा:
एकाच कंसात अंतर्लिखित झालेले सर्व कोन एकरूप असतात.
आकृतीमध्ये, जीवा LM ≅ जीवा LN आणि ∠L = 35°, तर
i. m(कंस MN) = किती?
ii. m(कंस LN) = किती?

आकृतीमध्ये, `square`PQRS हा चक्रीय चौकोन आहे. बाजू PQ ≅ बाजू RQ, ∠PSR = 110°, तर m(कंस QR) = किती?
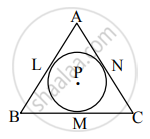
खालील आकृतीमध्ये, P केंद्र असलेले वर्तुळ ΔABC मध्ये अंतर्लिखित असून बाजू AB, बाजू BC व बाजू AC ला अनुक्रमे L, M व N बिंदूत स्पर्श करते. या वर्तुळाची त्रिज्या r आहे. सिद्ध करा, की : A(ΔABC) = `1/2`(AB + BC + AC) × r
`square`ABCD हा चक्रीय चौकोन आहे. m(कंस ABC) = 230°. तर ∠ABC, ∠CDA, ∠CBE, यांची मापे काढा.
सोबतच्या आकृतीत, `square`ABCD हा चक्रीय चौकोन आहे. m(कंस BC) = 90° आणि ∠DBC = 55°, तर ∠BCD चे माप काढा.