Advertisements
Advertisements
प्रश्न
An electron with kinetic energy 5 eV is incident on a hydrogen atom in its ground state. The collision
विकल्प
must be elastic
may be partially elastic
must be completely inelastic
may be completely inelastic
उत्तर
must be elastic.
The minimum energy required to excite a hydrogen atom from its ground state to 1st excited state is approximately 10 eV. As the incident electron energy is not sufficient for excitation of the hydrogen atom so electron will not get absorbed in the hydrogen atom so it can not be an inelastic collision. Also this collision can not be partially elastic because in an partially elestic collision, there is a net loss on kinetic energy. If the energy is lost then corresponding amount of heat shlould have been produced but it is not so which implies that the collision is completely elastic.
APPEARS IN
संबंधित प्रश्न
If Bohr’s quantisation postulate (angular momentum = nh/2π) is a basic law of nature, it should be equally valid for the case of planetary motion also. Why then do we never speak of quantisation of orbits of planets around the sun?
Find the wavelength of the electron orbiting in the first excited state in hydrogen atom.
Which wavelengths will be emitted by a sample of atomic hydrogen gas (in ground state) if electrons of energy 12.2 eV collide with the atoms of the gas?
Which of the following curves may represent the speed of the electron in a hydrogen atom as a function of trincipal quantum number n?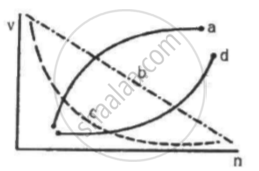
Let An be the area enclosed by the nth orbit in a hydrogen atom. The graph of ln (An/A1) against ln(n)
(a) will pass through the origin
(b) will be a straight line with slope 4
(c) will be a monotonically increasing nonlinear curve
(d) will be a circle
(a) Find the first excitation potential of He+ ion. (b) Find the ionization potential of Li++ion.
A group of hydrogen atoms are prepared in n = 4 states. List the wavelength that are emitted as the atoms make transitions and return to n = 2 states.
Find the maximum Coulomb force that can act on the electron due to the nucleus in a hydrogen atom.
A hydrogen atom in a state having a binding energy of 0.85 eV makes transition to a state with excitation energy 10.2 e.V (a) Identify the quantum numbers n of the upper and the lower energy states involved in the transition. (b) Find the wavelength of the emitted radiation.
A hydrogen atom in state n = 6 makes two successive transitions and reaches the ground state. In the first transition a photon of 1.13 eV is emitted. (a) Find the energy of the photon emitted in the second transition (b) What is the value of n in the intermediate state?
A gas of hydrogen-like ions is prepared in a particular excited state A. It emits photons having wavelength equal to the wavelength of the first line of the Lyman series together with photons of five other wavelengths. Identify the gas and find the principal quantum number of the state A.
Find the maximum angular speed of the electron of a hydrogen atom in a stationary orbit.
Suppose, in certain conditions only those transitions are allowed to hydrogen atoms in which the principal quantum number n changes by 2. (a) Find the smallest wavelength emitted by hydrogen. (b) List the wavelength emitted by hydrogen in the visible range (380 nm to 780 nm).
Find the temperature at which the average thermal kinetic energy is equal to the energy needed to take a hydrogen atom from its ground state to n = 3 state. Hydrogen can now emit red light of wavelength 653.1 nm. Because of Maxwellian distribution of speeds, a hydrogen sample emits red light at temperatures much lower than that obtained from this problem. Assume that hydrogen molecules dissociate into atoms.
Show that the ratio of the magnetic dipole moment to the angular momentum (l = mvr) is a universal constant for hydrogen-like atoms and ions. Find its value.
The Balmer series for the H-atom can be observed ______.
- if we measure the frequencies of light emitted when an excited atom falls to the ground state.
- if we measure the frequencies of light emitted due to transitions between excited states and the first excited state.
- in any transition in a H-atom.
- as a sequence of frequencies with the higher frequencies getting closely packed.
Let En = `(-1)/(8ε_0^2) (me^4)/(n^2h^2)` be the energy of the nth level of H-atom. If all the H-atoms are in the ground state and radiation of frequency (E2 - E1)/h falls on it ______.
- it will not be absorbed at all.
- some of atoms will move to the first excited state.
- all atoms will be excited to the n = 2 state.
- no atoms will make a transition to the n = 3 state.
Positronium is just like a H-atom with the proton replaced by the positively charged anti-particle of the electron (called the positron which is as massive as the electron). What would be the ground state energy of positronium?
