Advertisements
Advertisements
प्रश्न
AP: 10, 6, 2,... के प्रथम 16 पदों का योग ______ है।
विकल्प
–320
320
–352
–400
उत्तर
AP: 10, 6, 2,... के प्रथम 16 पदों का योग –320 है।
स्पष्टीकरण:
दिया गया है, AP is 10, 6, 2,...
यहाँ,
पहला पद a = 10,
सामान्य अंतर,
d = – 4
∴ S16 = `16/2[2a + (16 - 1)d]` ...`[∵ S_n = n/2[2a + (n - 1)d]]`
= 8[2 × 10 + 15(– 4)]
= 8(20 – 60)
= 8(– 40)
= – 320
APPEARS IN
संबंधित प्रश्न
एक A.P. में, l = 28, S = 144 और कुल 9 पद हैं। a ज्ञात कीजिए।
ऐसे प्रथम 40 धन पूर्णांकों का योग ज्ञात कीजिए जो 6 से विभाज्य हैं।
8 के प्रथम 15 गुणजों का योग ज्ञात कीजिए।
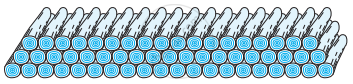
200 लट्ठों (logs) को ढेरी के रूप में इस प्रकार रखा जाता है : सबसे नीचे वाली पंक्ति में 20 लट्ठे, उससे अगली पंक्ति में 19 लट्ठे, उससे अगली पंक्ति में 18 लट्ठे, इत्यादि (देखिए आकृति)। ये 200 लठ्ठे कितनी पंक्तियों में रखे गए हैं तथा सबसे ऊपरी पंक्ति में कितने लट्ठे हैं?
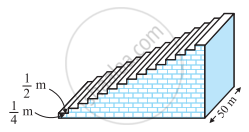
एक फुटबॉल के मैदान में एक छोटा चबूतरा है जिसमें 15 सीढ़ियाँ बनी हुई हैं। इन सीढ़ियों में से प्रत्येक की लंबाई 50 m है और वह ठोस कंक्रीट (concrete) की बनी है। प्रत्येक सीढ़ी में `1/4` m की चढ़ाई है और `1/2` m का फैलाव (चौड़ाई) है। (देखिए आकृति)।इस चबूतरे को बनाने में लगी कंक्रीट का कुल आयतन परिकलित कीजिए।
[संकेत: पहली सीढ़ी को बनाने में लगी कंक्रीट का आयतन = `1/4 xx 1/2 xx 50` m3 है।]
प्रथम 100 प्राकृत संख्याओं के योग को ज्ञात करने से संबद्ध प्रसिद्ध गणितज्ञ ______ है।
AP: –2, –7, –12,... का कौन-सा पद –77 है? पद –77 तक इस AP का योग ज्ञात कीजिए।
यदि Sn किसी AP के प्रथम n पदों का योग व्यक्त करता है, तो सिद्ध कीजिए कि S12 = 3(S8 – S4) है।
दर्शाइए कि उस AP का योग, जिसका प्रथम पद a, द्वितीय पद b और अंतिम पद c हो, `((a + c)(b + c - 2a))/(2(b - a))` के बराबर है।
समीकरण – 4 + (−1) + 2 + ... + x = 437 को हल कीजिए।
