Advertisements
Advertisements
प्रश्न
समीकरण – 4 + (−1) + 2 + ... + x = 437 को हल कीजिए।
उत्तर
दिया गया समीकरण है,
– 4 + (–1) + 2 + ... + x = 437 ...(i)
यहाँ, – 4 – 1 + 2 + ... + x पहले पद = – 4 के साथ एक एपी बनाता है,
सामान्य अंतर = – 1 – (– 4) = 3,
an = l = x
∵ किसी AP का n वाँ पद,
an = l = a + (n – 1)d
⇒ x = – 4 + (n – 1)3 ...(ii)
⇒ `(x + 4)/3` = n – 1
⇒ n = `(x + 7)/3`
∴ एक AP का योग,
Sn = `n/2[2a + (n - 1)d]`
Sn = `(x + 7)/(2 xx 3)[2(-4) + ((x + 4)/3) * 3]`
= `(x + 7)/(2 xx 3)(-8 + x + 4)`
= `((x + 7)(x - 4))/(2 xx 3)`
समीकरण (i) से,
Sn = 437
⇒ `((x + 7)(x - 4))/(2 xx 3)` = 437
⇒ x2 + 7x – 4x – 28 = 874 × 3
⇒ x2 + 3x – 2650 = 0
x = `(-3 +- sqrt((3)^2 - 4(-2650)))/2` ...[द्विघात सूत्र द्वारा]
= `(-3 +- sqrt(9 + 10600))/2`
= `(-3 +- sqrt(10609))/2`
= `(-3 +- 103)/2`
= `100/2, (-106)/2`
= 50, – 53
यहाँ, x ऋणात्मक नहीं हो सकता अर्थात x ≠ – 53
साथ ही x = – 53 के लिए n ऋणात्मक होगा जो संभव नहीं है।
अत:, x का अभीष्ट मान 50 है।
APPEARS IN
संबंधित प्रश्न
निम्नलिखित समांतर श्रेढ़ी का योग ज्ञात कीजिए:
0.6, 1.7, 2.8, ....,100 पदों तक
8 के प्रथम 15 गुणजों का योग ज्ञात कीजिए।
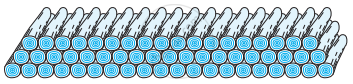
200 लट्ठों (logs) को ढेरी के रूप में इस प्रकार रखा जाता है : सबसे नीचे वाली पंक्ति में 20 लट्ठे, उससे अगली पंक्ति में 19 लट्ठे, उससे अगली पंक्ति में 18 लट्ठे, इत्यादि (देखिए आकृति)। ये 200 लठ्ठे कितनी पंक्तियों में रखे गए हैं तथा सबसे ऊपरी पंक्ति में कितने लट्ठे हैं?
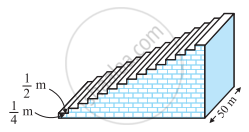
एक फुटबॉल के मैदान में एक छोटा चबूतरा है जिसमें 15 सीढ़ियाँ बनी हुई हैं। इन सीढ़ियों में से प्रत्येक की लंबाई 50 m है और वह ठोस कंक्रीट (concrete) की बनी है। प्रत्येक सीढ़ी में `1/4` m की चढ़ाई है और `1/2` m का फैलाव (चौड़ाई) है। (देखिए आकृति)।इस चबूतरे को बनाने में लगी कंक्रीट का कुल आयतन परिकलित कीजिए।
[संकेत: पहली सीढ़ी को बनाने में लगी कंक्रीट का आयतन = `1/4 xx 1/2 xx 50` m3 है।]
किसी AP का प्रथम पद −5 और अंतिम पद 45 है। यदि इस AP के पदों का योग 120 हो, तो पदों की संख्या और सार्व अंतर ज्ञात कीजिए।
यदि Sn किसी AP के प्रथम n पदों का योग व्यक्त करता है, तो सिद्ध कीजिए कि S12 = 3(S8 – S4) है।
ज्ञात कीजिए :
1 से 500 तक के उन पूर्णांकों का योग जो 2 के भी गुणज हैं और 5 के भी गुणज हैं।
100 और 200 के बीच के उन पूर्णांकों का योग ज्ञात कीजिए, जो
- 9 से विभाज्य हैं।
- 9 से विभाज्य नहीं हैं।
[संकेत (ii) : ये संख्याएँ होंगी : कुल संख्याएँ – 9 से विभाज्य संख्याएँ]
किसी AP के 11 वें पद का 18 वे पद से अनुपात 2 : 3 है। 5 वें पद का 21 वें पद से अनुपात ज्ञात कीजिए तथा साथ ही प्रथम पाँच पदों के योग का प्रथम 21 पदों के योग से अनुपात ज्ञात कीजिए।
दर्शाइए कि उस AP का योग, जिसका प्रथम पद a, द्वितीय पद b और अंतिम पद c हो, `((a + c)(b + c - 2a))/(2(b - a))` के बराबर है।
