Advertisements
Advertisements
प्रश्न
बिंदु (1, 2) से होकर जाने वाली एक प्रकाश किरण x-अक्ष के बिंदु A से परावर्तित होती है और परावर्तित किरण बिंदु (5, 3) से होकर जाती है। A के निर्देशांक ज्ञात कीजिए।
उत्तर
मान लीजिए BC, x-अक्ष के अनुदिश उस बिंदु के निर्देशांक A (a, 0) है। AN इस पर लंब है। PA एक आपतित किरण है और AQ परावर्तित किरण है।
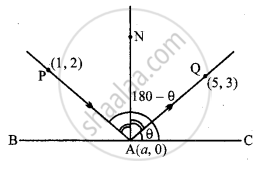
⇒ आपतित कोण PAN = परावर्तित कोण NAQ
⇒ ∠PAB = ∠QAC
⇒ यदि QA का झुकाव 0 हो तो PA का झुकाव 180 – θ होगा।
QA की ढाल जबकि Q(5, 3) और A(a, 0) हो, तो
`tan θ = (0 - 3)/("a" - 5) = (-3)/("a" - 5)`
PA की ढाल जबकि P(1, 2) और A(a, 0) हो, तब
tan (180° - θ) = `(0 - 2)/("a" - 1)`
tan (180° - θ) = − tan θ
∴ `(-2)/("a" - 1) = (-3)/("a" - 5) = 3/("a" - 5)`
या −2(a − 5) = 3(a − 1)
या −2a + 10 = 3a − 3
या 5a = 13
या a = `13/5`
∴ बिंदु A के निर्देशांक `(13/5, 0)` है।
APPEARS IN
संबंधित प्रश्न
बिंदु (−1, 1) की रेखा 12(x + 6) = 5(y – 2) से दूरी ज्ञात कीजिए।
x-अक्ष पर बिंदुओं को ज्ञात कीजिए जिनकी रेखा `"x"/3 + "y"/4 = 1` से दूरियाँ 4 इकाई हैं।
समांतर रेखाओं के बीच की दूरी ज्ञात कीजिए:
l(x +y) + p = 0 और l(x + y) – r = 0
रेखा 3x – 4y + 2 = 0 के समांतर और बिंदु (−2, 3) से जाने वाली रेखा का समीकरण ज्ञात कीजिए।
बिंदु (2, 3) से जाने वाली दो रेखाएँ परस्पर 60° के कोण पर प्रतिच्छेद करती हैं। यदि एक रेखा की ढाल 2 है तो दूसरी रेखा का समीकरण ज्ञात कीजिए।
बिंदुओं (3, 4) और (−1, 2) को मिलाने वाली रेखाखंड के लंब समद्विभाजक रेखा का समीकरण ज्ञात कीजिए।
y-अक्ष पर कौन से बिंदु ऐसे हैं, जिनकी रेखा `"x"/3 + "y"/4 = 1` से दूरी 4 इकाई है।
मूल बिंदु से बिंदुओं (cos θ, sin θ) और (cos ϕ, sin ϕ) को मिलाने वाली रेखा की लांबिक दूरी ज्ञात कीजिए।
रेखाओं x – 7y + 5 = 0 और 3x + y = 0 के प्रतिच्छेद बिंदु से खींची गई और y-अक्ष के समांतर रेखा का समीकरण ज्ञात कीजिए।
बिंदु (1, 2) से रेखा 4x + 7y + 5 = 0 की 2x – y = 0 के अनुदिश दूरी ज्ञात करो।
बिंदु (−1, 2) से खींची जा सकने वाली उस रेखा की दिशा ज्ञात कीजिए जिसका रेखा x + y = 4 से प्रतिच्छेदन बिंदु दिए बिंदु से 3 इकाई की दूरी पर है।
यदि एक वर बिंदु P(x, y) की रेखाओं x + y – 5 = 0 और 3x – 2y + 7 = 0 से लांबिक दूरियों का योग सदैव 10 रहे तो दर्शाइए कि P अनिवार्य रूप से एक रेखा पर गमन करता है।
