Advertisements
Advertisements
प्रश्न
Calculate the distance of an object of height h from a concave mirror of radius of curvature 20 cm, so as to obtain a real image of magnification 2. Find the location of the image also.
उत्तर
Given: Radius of curvature of mirror = 20 cm
∴ Focal length of mirror, f = −10 cm
Since the image is real,
Magnification of image, m = −2
`m=-v/u`
`=>-2=-v/u`
`=>v=2u`
Using mirror formula,
`1/f=1/v+1/u=1/(2u)+1/u=3/(2u)`
`=>u=3/2 f=3/2xx(-10)=-15cm`
∴v=2u=−30 cm
Therefore, the distance of the object is 15 cm in front of the mirror and the position of the image is 30 cm in front of the mirror.
संबंधित प्रश्न
Use the mirror equation to show that an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
Use the mirror equation to show that a convex mirror always produces a virtual image independent of the location of the object.
Use the mirror equation to deduce that the virtual image produced by a convex mirror is always diminished in size and is located between the focus and the pole.
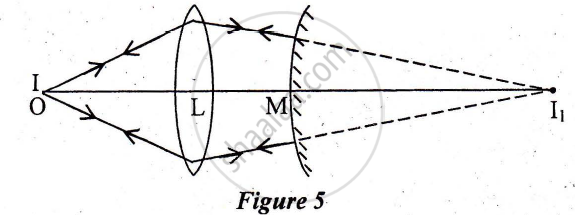
A point object O is placed at a distance of 15cm from a convex lens L of focal length 1 Ocm as shown in Figure 5 below. On the other side of the lens, a convex mirror M is placed such that its distance from the lens is equal to the focal length of the lens. The final image formed by this combination is observed to coincide with the object O. Find the focal length of the convex mirror
Use the mirror equation to show a convex mirror always produces a virtual image independent of the location of the object ?
The rays of different colours fail to converge at a point after going through a converging lens. This defect is called
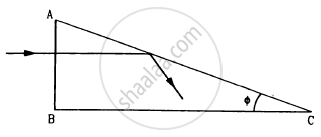
A light ray is incident normally on the face AB of a right-angled prism ABC (μ = 1.50) as shown in figure. What is the largest angle ϕ for which the light ray is totally reflected at the surface AC?
For paraxial rays, show that the focal length of a spherical mirror is one-half of its radius of curvature.
A point object is placed at a distance of 20 cm from a thin plano-convex lens of focal length 15 cm, if the plane surface is silvered. The image will form at:
When a clock is viewed in a mirror, the needles exhibit a time which appears to be 8:20. Then the actual time will be:
