Advertisements
Advertisements
प्रश्न
A light ray is incident normally on the face AB of a right-angled prism ABC (μ = 1.50) as shown in figure. What is the largest angle ϕ for which the light ray is totally reflected at the surface AC?
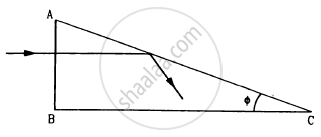
उत्तर
Given,
Refractive index (μ) of prism = 1.50
Let us take θc as the critical angle for the glass.
So, According to Snell's law,
\[\frac{\sin \theta_c}{\sin 90^\circ } = \frac{1}{\mu}\]
\[\Rightarrow \sin \theta c = \frac{1}{1 . 5} = \frac{2}{3}\]
\[\Rightarrow \theta_c = \sin^{- 1} \frac{2}{3}\]
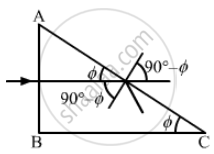
Condition for total internal reflection: 90° − \[\phi\] θc
⇒ \[\phi\] < 90° - θc
\[\Rightarrow \theta_c = \sin^{- 1} \frac{2}{3}\]
\[\Rightarrow \phi < \cos^{- 1} \left( \frac{2}{3} \right)\]
Hence, the largest angle for which light is totally reflected at the surface AC is \[\cos^{- 1} \left( \frac{2}{3} \right)\]
APPEARS IN
संबंधित प्रश्न
Calculate the distance of an object of height h from a concave mirror of radius of curvature 20 cm, so as to obtain a real image of magnification 2. Find the location of the image also.
a) Give two reasons to explain why reflecting telescopes are preferred over refracting type.
Use the mirror equation to show that an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
Use the mirror equation to deduce that an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.
Using mirror formula, explain why does a convex mirror always produce a virtual image.
Use the mirror equation to show a convex mirror always produces a virtual image independent of the location of the object ?
Can a plane mirror ever form a real image?
following Figure shows two rays A and B being reflected by a mirror and going as A' and B'. The mirror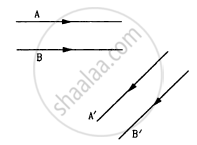
The rays of different colours fail to converge at a point after going through a converging lens. This defect is called
A cylindrical vessel of diameter 12 cm contains 800π cm3 of water. A cylindrical glass piece of diameter 8.0 cm and height 8.0 cm is placed in the vessel. If the bottom of the vessel under the glass piece is seen by the paraxial rays (see figure), locate its image. The index of refraction of glass is 1.50 and that of water is 1.33.

A small object is placed at the centre of the bottom of a cylindrical vessel of radius 3 cm and height 4 cm filled completely with water. Consider the ray leaving the vessel through a corner. Suppose this ray and the ray along the axis of the vessel are used to trace the image. Find the apparent depth of the image and the ratio of real depth to the apparent depth under the assumptions taken. Refractive index of water = 1.33.
Find the maximum angle of refraction when a light ray is refracted from glass (μ = 1.50) to air.
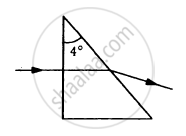
Find the angle of deviation suffered by the light ray shown in figure. The refractive index μ = 1.5 for the prism material.
A light ray, going through a prism with the angle of prism 60°, is found to deviate by 30°. What limit on the refractive index can be put from these data?
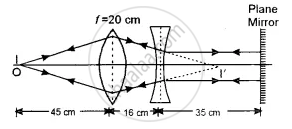
The figure below shows the positions of a point object O, two lenses, a plane mirror and the final image I which coincides with the object. The focal length of the convex lens is 20 cm. Calculate the focal length of the concave lens.
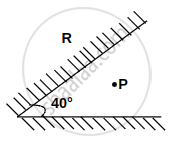
Two plane mirrors are inclined at an angle of 40°. The possible number of images of an object placed at point P would be?
A point object is placed at a distance of 30 cm from a convex mirror of a focal length of 30 cm. What is the separation between the image and the object?
