Advertisements
Advertisements
प्रश्न
Derive the work done in an isothermal process.
उत्तर
Work done in an isothermal process: Consider an ideal gas which is allowed to expand quasi-statically at a constant temperature from an initial state (Pi, Vi) to the final state (Pf, Vf). We can calculate the work done by the gas during this process. The work done by the gas,
W = `int_("V"_"i")^("V"_"f") "PdV"` ........(1)
As the process occurs quasi-statically, at every stage the gas is at equilibrium with the surroundings. Since it is in equilibrium at every stage the ideal gas law is valid. Writing pressure in terms of volume and temperature,
P = `(µ"RT")/"V"` ................(2)
Substituting equation (2) in (1) we get
W = `int_("V"_"i")^("V"_"f") (µ"RT")/"V" "d"V`
W = `µ"RT" int_("V"_"i")^("V"_"f") "dV"/"V"` .........(3)
In equation (3), we take uRT out of the integral, since it is constant throughout the isothermal process.
By performing the integration in equation (3), we get
W = `µ"RT" ln ("V"_"f"/"V"_"i")` ..........(4)
Since we have an isothermal expansion, `"V"_"f"/"V"_"i" > 1`, so ln `("V"_"f"/"V"_"i") > 0` As a result the work done by the gas during an isothermal expansion is positive.
The above result in equation (4) is true for isothermal compression also. But in an isothermal compression `"V"_"f"/"V"_"i" < 1`, so ln `("V"_"f"/"V"_"i") < 0`.
As a result, the work done on the gas is an isothermal compression is negative.
In the PV diagram, the work done during the isothermal expansion is equal to the area under the graph.


Work done in an isothermal process
Similarly, for an isothermal compression, the area under the PV graph is equal to the work done on the gas which turns out to be the area with a negative sign.
APPEARS IN
संबंधित प्रश्न
Give an example of some familiar process in which heat is added to an object, without changing its temperature.
Draw a p-V diagram of the reversible process.
3 mole of a gas at temperature 400 K expands isothermally from an initial volume of 4 litres to a final volume of 8 litres. Find the work done by the gas. (R = 8.31 J mol-1 K-1)
An ideal gas of volume 2 L is adiabatically compressed to (1/10)th of its initial volume. Its initial pressure is 1.01 x 105 Pa, calculate the final pressure. (Given 𝛾 = 1.4)
When a cycle tyre suddenly bursts, the air inside the tyre expands. This process is ____________.
In an isochoric process, we have ____________.
Derive the work done in an adiabatic process.
What are the limitations of the first law of thermodynamics?
For an isothermal expansion of a perfect gas, the value of `(Delta "P")/"P"` is equal to ____________.
Consider P-V diagram for an ideal gas shown in figure.
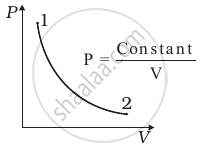
Out of the following diagrams (figure), which represents the T-P diagram?
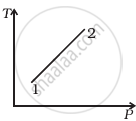 (i) |
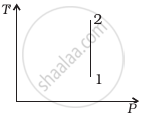 (ii) |
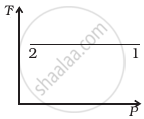 (iii) |
 (iv) |
