Advertisements
Advertisements
प्रश्न
दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।
निम्न अवरोधों के अंतर्गत Z = -x + 2y का अधिकतमीकरण कीजिए:
x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
उत्तर
बाधाओं की प्रणाली इस प्रकार है:
x ≥ 3 ...(i)
x + y ≥ 5 ...(ii)
x + 2y ≥ 6 ...(iii)
और y ≥ 0 ...(iv)
माना l1 : x = 3
l2 : x + y = 5
l3 : x + 2y = 6
l4 : y = 0
चित्र में छायांकित क्षेत्र बाधाओं (i) से (iv) की प्रणाली द्वारा निर्धारित व्यवहार्य क्षेत्र है।
कोने बिंदु C(6, 0), E(4, 1) और F(3, 2) हैं।
बिन्दु विधि लागू करने पर, हमें यह प्राप्त होता है।
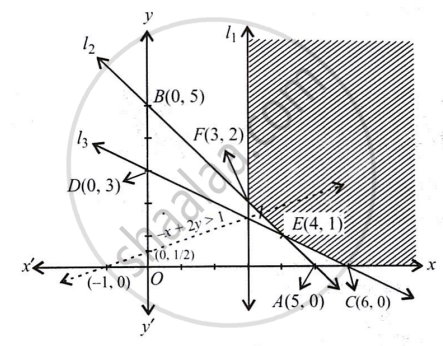
| बिन्दु | Z के संगत मान |
| (6, 0) | -6 |
| (4, 1) | -2 |
| (3, 2) | 1 |
ऐसा प्रतीत होता है, कि (3, 2) पर Z अधिकतम = 1 है।
लेकिन सुसंगत क्षेत्र असीमित है, इसलिए, हम असमानता का ग्राफ -x + 2y > 1 खींचते हैं।
चूँकि - x + 2y > 1 द्वारा निरूपित अर्ध-तल में सुसंगत क्षेत्र के साथ उभयनिष्ठ बिंदु हैं।
∴ Z अधिकतम ≠ 1
अतः Z का कोई अधिकतम मान नहीं है।
APPEARS IN
संबंधित प्रश्न
ग्राफ़ीय विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए:
निम्न अवरोधों के अंतर्गत Z = 5x + 3y का अधिकतमीकरण कीजिए:
3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
ग्राफ़ीय विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए:
निम्न अवरोधों के अंतर्गत Z = 3x + 5y का न्यूनतमीकरण कीजिए:
x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0
ग्राफ़ीय विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए:
निम्न अवरोधों के अंतर्गत Z = 3x + 2y का न्यूनतमीकरण कीजिए:
x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0
ग्राफ़ीय विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए:
निम्न अवरोधों के अंतर्गत Z = x + 2y का न्यूनतमीकरण कीजिए:
2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0
दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।
निम्न अवरोधों के अंतर्गत Z = 5x + 10y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए:
x + 2y ≤ 120, x + y ≥ 60, x - 2y ≥ 0, x, y ≥ 0.
दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।
निम्न अवरोधों के अंतर्गत Z = x + 2y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए:
x + 2y ≥ 100, 2x - y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.
दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।
निम्न अवरोधों के अंतर्गत Z = x + y का अधिकतमीकरण कीजिए:
x - y ≤ -1, -x + y ≤ 0, x, y ≥ 0.
