Advertisements
Advertisements
प्रश्न
Draw a labelled diagram to show different trajectories of a satellite depending upon the tangential projection speed.
उत्तर
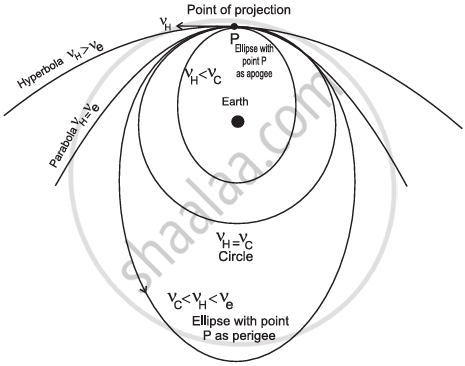
vh = horizontal speed of projection
vc = critical velocity
ve = escape velocity
APPEARS IN
संबंधित प्रश्न
Consider earth satellites in circular orbits. A geostationary satellite must be at a height of about 36000 km from the earth's surface. Will any satellite moving at this height be a geostationary satellite? Will any satellite moving at this height have a time period of 24 hours?
Two satellites A and B move round the earth in the same orbit. The mass of B is twice the mass of A.
At what rate should the earth rotate so that the apparent g at the equator becomes zero? What will be the length of the day in this situation?
A pendulum having a bob of mass m is hanging in a ship sailing along the equator from east to west. When the ship is stationary with respect to water the tension in the string is T0. (a) Find the speed of the ship due to rotation of the earth about its axis. (b) Find the difference between T0 and the earth's attraction on the bob. (c) If the ship sails at speed v, what is the tension in the string? Angular speed of earth's rotation is ω and radius of the earth is R.
A Mars satellite moving in an orbit of radius 9.4 × 103 km takes 27540 s to complete one revolution. Calculate the mass of Mars.
What is the true weight of an object in a geostationary satellite that weighed exactly 10.0 N at the north pole?
Choose the correct option.
The binding energy of a satellite revolving around the planet in a circular orbit is 3 × 109 J. It's kinetic energy is ______.
Answer the following question in detail.
State any four applications of a communication satellite.
Answer the following question in detail.
Obtain an expression for the binding energy of a satellite revolving around the Earth at a certain altitude.
Describe how an artificial satellite using a two-stage rocket is launched in an orbit around the Earth.
Solve the following problem.
Calculate the speed of a satellite in an orbit at a height of 1000 km from the Earth’s surface.
(ME = 5.98 × 1024 kg, R = 6.4 × 106 m)
Solve the following problem.
Calculate the value of the universal gravitational constant from the given data. Mass of the Earth = 6 × 1024 kg, Radius of the Earth = 6400 km, and the acceleration due to gravity on the surface = 9.8 m/s2.
A body weighs 5.6 kg wt on the surface of the Earth. How much will be its weight on a planet whose mass is 7 times the mass of the Earth and radius twice that of the Earth’s radius?
The ratio of energy required to raise a satellite of mass 'm' to a height 'h' above the earth's surface of that required to put it into the orbit at same height is ______.
[R = radius of the earth]
If a body weighing 40 kg is taken inside the earth to a depth to radius of the earth, then `1/8`th the weight of the body at that point is ______.
Two satellites A and B go round a planet P in circular orbits having radii 4R and R respectively. If the speed of the satellite A is 3v, the speed of satellite B is ____________.
Reason of weightlessness in a satellite is ____________.
Two satellites of masses m and 4m orbit the earth in circular orbits of radii 8r and r respectively. The ratio of their orbital speeds is ____________.
Out of following, the only correct statement about satellites is ____________.
The ratio of energy required to raise a satellite to a height `(2R)/3` above earth's surface to that required to put it into the orbit at the same height is ______.
R = radius of the earth
A satellite of mass 'm', revolving round the earth of radius 'r' has kinetic energy (E). Its angular momentum is ______.
A satellite is to revolve round the earth in a circle of radius 9600 km. The speed with which this satellite be projected into an orbit, will be ______.
A geostationary satellite is orbiting the earth at a height 6R above the surface of the earth, where R is the radius of the earth. This time period of another satellite at a height (2.5 R) from the surface of the earth is ______.
The period of revolution of a satellite is ______.
A satellite is revolving in a circular orbit at a height 'h' above the surface of the earth of radius 'R'. The speed of the satellite in its orbit is one-fourth the escape velocity from the surface of the earth. The relation between 'h' and 'R' is ______.
A satellite is revolving around a planet in a circular orbit close to its surface and ρ is the mean density and R is the radius of the planet, then the period of ______.
(G = universal constant of gravitation)
