Advertisements
Advertisements
प्रश्न
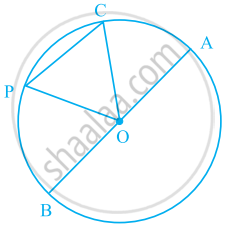
एक वृत्त की त्रिज्या `sqrt2` cm है। 2 cm लंबाई वाली जीवा द्वारा यह वृत्त दो वृत्त-खंडों में विभाजित किया जाता है। सिद्ध कीजिए कि इस जीवा द्वारा दीर्घ वृत्त-खंड के किसी बिंदु पर बना कोण 45° है।
उत्तर
O केंद्र वाला एक वृत्त खींचिए। मान लीजिए कि AB = 2 सेमी वृत्त की एक जीवा है। एक जीवा AB को रेखा OM द्वारा दो बराबर खंडों में विभाजित किया जाता है।
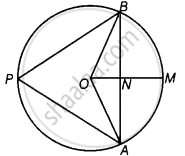
सिद्ध करना है - ∠APB = 45°
यहाँ, AN = NB = 1 सेमी
तथा OB = `sqrt(2)` सेमी
ΔONB में, OB2 = ON2 + NB2 ...[पाइथागोरस प्रमेय का प्रयोग कीजिए]
⇒ `(sqrt(2))^2 = ON^2 + (1)^2`
⇒ ON2 = 2 – 1 = 1
⇒ ON = 1 सेमी ...[सकारात्मक वर्गमूल लेना, क्योंकि दूरी हमेशा धनात्मक होती है।]
साथ ही, ∠ONB = 90° ...[ON जीवा AB का लंब समद्विभाजक है।]
∴ ∠NOB = ∠NBO = 45°
इसी प्रकार, ∠AON = 45°
अब, ∠AOB = ∠AON + ∠NOB
= 45° + 45°
= 90°
हम जानते हैं कि, जीवा वृत्त पर एक कोण अंतरित करती है जो केंद्र में अंतरित कोण का आधा होता है।
∴ `∠APB = 1/2 ∠AOB`
= `90^circ/2`
= 45°
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
एक वृत्त, जिस तल पर स्थित है, उसे _______ भागों में विभाजित करता है।
संलग्न आकृति देखकर लिखिए:
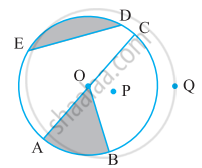
एक जीवा
संलग्न आकृति देखकर लिखिए:
अभ्यंतर में दो बिंदु
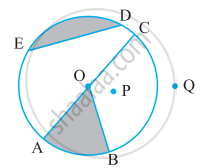
संलग्न आकृति देखकर लिखिए:
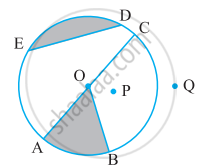
एक वृतखंड
किसी वृत्त का AD एक व्यास है और AB एक जीवा है। यदि AD = 34 cm, AB = 30 cm है, तो वृत्त के केंद्र से AB की दूरी है
यदि AB = 12 cm, BC = 16 cm और AB रेखाखंड BC पर लंब है, तो A, B और C से होकर जाने वाले वृत्त की त्रिज्या है
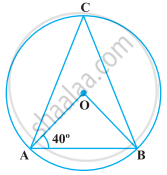
निम्नलिखित आकृति में, यदि ∠OAB = 40° है, तो ∠ACB बराबर है
ABCD एक ऐसा चक्रीय चतुर्भुज है कि AB इस चतुर्भुज के परिगत वृत्त का एक व्यास है तथा ∠ADC = 140° है। तब, ∠BAC बराबर है
यदि एक वृत्त PXAQBY की एक जीवा AB का लंब समद्विभाजक वृत्त को P और Q बिंदुओं पर प्रतिच्छेद करता है, तो सिद्ध कीजिए कि चाप PXA ≅ चाप PYB हैं।
आकृति में O एक वृत्त का केंद्र है। त्रिज्याखंड OAC और OPB को छायांकित'कीजिए।