Advertisements
Advertisements
प्रश्न
यदि एक चक्रीय चतुर्भुज ABCD के सम्मुख कोणों के समद्विभाजक इस चतुर्भुज के परिगत वृत्त को P और Q, बिंदुओं पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि PQ इस वृत्त का व्यास है।
उत्तर
दिया गया है - ABCD एक चक्रीय चतुर्भुज है।
DP और QB क्रमश : ∠D और ∠B के समद्विभाजक हैं।
सिद्ध करना है - PQ एक वृत्त का व्यास है।
रचना - QD और QC को मिलाइए।
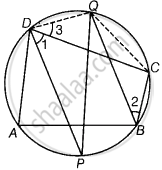
उपपत्ति - चूँकि, ABCD एक चक्रीय चतुर्भुज है।
∴ ∠CDA + ∠CBA = 180° ...[चक्रीय चतुर्भुज के सम्मुख कोणों का योग 180° है।]
दोनों पक्षों को 2 से भाग देने पर, हम पाते हैं।
`1/2 ∠CDA + 1/2 ∠CBA = 1/2 xx 180^circ = 90^circ`
⇒ ∠1 + ∠2 = 90° ...(i) `[∠1 = 1/2 ∠CDA और ∠2 = 1/2 ∠CBA]`
लेकिन ∠2 = ∠3 [समान वृत्तखंड QC में कोण बराबर होते हैं।] ...(ii)
∠1 + ∠3 = 90°
समीकरण (i) और (ii) से,
∠PDQ = 90°
इसलिए, PQ एक वृत्त का व्यास है, क्योंकि वृत्त का व्यास है।
परिधि पर समकोण बनाता है।
APPEARS IN
संबंधित प्रश्न
याद कीजिए कि दो वृत्त सर्वांगसम होते हैं, यदि उनकी त्रिज्याएँ बराबर हों। सिद्ध कीजिए कि सर्वांगसम वृत्तों की बराबर जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करती हैं।
सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों की जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करें, तो जीवाएँ बराबर होती हैं।
यदि BM और CN त्रिभुज ABC की भुजाओं AC और AB पर खींचे गए लंब हैं, तो सिद्ध कीजिए कि बिंदु B, C, M और N चक्रीय हैं।
केंद्रों O और O' वाले दो वृत्त बिंदुओं A और B पर प्रतिच्छेद करते हैं। A (या B) से होकर एक रेखा PQ रेखाखंड OO' के समांतर खींची जाती है, जो वृत्तों को P और Q पर प्रतिच्छेद करती है। सिद्ध कीजिए कि PQ = 2 OO' है।
यदि P, Q और R क्रमश : एक त्रिभुज की BC, CA और AB भुजाओं के मध्य-बिंदु हैं तथा AD शीर्ष A से BC पर लंब है, तो सिद्ध कीजिए कि बिंदु P, Q, R और D चक्रीय है।
