Advertisements
Advertisements
प्रश्न
निम्नलिखित आकृति में, AB और CD एक वृत्त की दो जीवाएँ हैं, जो E पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि AEC = `1/2` (चाप CXA द्वारा केंद्र पर अंतरित कोण + चाप DYB द्वारा केंद्र पर अंतरित कोण) है।
उत्तर
दिया गया है - एक आकृति में, दो जीवाएँ AB और CD परस्पर बिंदु E पर प्रतिच्छेद करती हैं।
साबित करने के लिए - ∠AEC = `1/2` ...[चाप C × A द्वारा केंद्र पर बनाया गया कोण + चाप DYB द्वारा केंद्र में बनाया गया कोण]
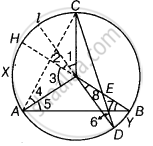
रचना - वृत्त पर बिंदुओं l और H पर DO और BQ रेखाओं का विस्तार करें। एसी भी ज्वाइन करें।
उपपत्ति - हम जानते हैं कि, एक वृत्त में, एक चाप द्वारा केंद्र पर बनाया गया कोण, वृत्त के शेष भाग पर बनाए गए कोण का दुगुना होता है।
∴ ∠1 = 2∠6 ...(i)
और ∠3 = 2∠7 ...(ii)
ΔAOC में, OC = OA ...[दोनों वृत्त की त्रिज्या हैं।]
∠OCA = ∠4 ...[समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
साथ ही, ∠AOC + ∠OCA + ∠4 = 180° ...[त्रिभुज के कोण योग गुण से]
⇒ ∠AOC + ∠4 + ∠4 = 180°
⇒ ∠AOC = 180° – 2∠4 ...(iii)
अब, ΔAEC में, ∠AEC + ∠ECA + ∠CAE = 180° ...[त्रिकोण के कोण गुण योग के अनुसार]
⇒ ∠AEC = 180° – (∠ECA + ∠CAE)
⇒ ∠AEC = 180° – [(∠ECO + ∠OCA) + ∠CAO + ∠OAE]
= 180° – (∠6 + ∠4 + ∠4 + ∠5) ...[∠OCD में, ∠6 = ∠ECO बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।]
= 180° – (2∠4 + ∠5 + ∠6)
= 180° – (180° – ∠AOC + ∠7 + ∠6) ...[समीकरण (iii) से और ΔAOB में, ∠5 = ∠7, क्योंकि (समान भुजाओं के सम्मुख कोण बराबर होते हैं।)]
= `∠AOC - (∠3)/2 - (∠1)/2` ...[समीकरण (i) और (ii) से]
= `∠AOC - (∠1)/2 - (∠2)/2 - (∠3)/2 + (∠2)/2` ...`["जोड़ना और घटाना" (∠2)/2]`
= `∠AOC - 1/2 (∠1 + ∠2 + ∠3) + (∠8)/2` ...[∵ ∠2 = ∠8 शीर्षाभिमुख कोण]
= `∠AOC - (∠AOC)/2 + (∠DOB)/2`
⇒ `∠AEC = 1/2 (∠AOC + ∠DOB)`
= `1/2` ...[चाप CXA द्वारा केंद्र पर अंतरित कोण + चाप DYB द्वारा केंद्र पर अंतरित कोण]
APPEARS IN
संबंधित प्रश्न
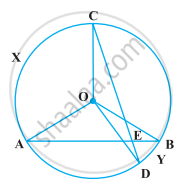
आकृति में, केंद्र O वाले एक वृत्त पर तीन बिन्दु A, B और C इस प्रकार हैं कि ∠BOC = 30० तथा ∠AOB = 60० है। यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिंदु है, तो ∠ADC ज्ञात कीजिए।

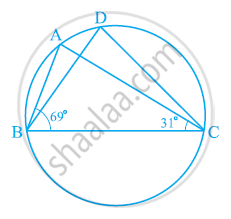
आकृति में, ∠ABC = 69° और ∠ACB = 31° हो, तो ∠BDC ज्ञात कीजिए।
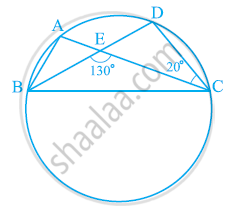
आकृति में, एक वृत्त पर A, B, C और D चार बिंदु हैं। AC और BD एक बिंदु E पर इस प्रकार प्रतिच्छेद करते हैं कि ∠BEC = 130° तथा ∠ECD = 20° है। ∠BAC ज्ञात कीजिए।
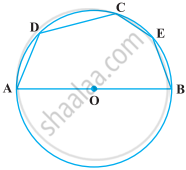
निम्नलिखित आकृति में, यदि AOB एक व्यास है और ∠ADC = 120° है, तो ∠CAB = 30° है।
यदि एक वृत्त के चाप AXB और CYD सर्वांगसम हैं तो AB और CD का अनुपात ज्ञात कीजिए।
किसी वृत्त की एक जीवा उसकी त्रिज्या के बराबर है। इस जीवा द्वारा दीर्घ वृत्तखंड में किसी बिंदु पर अंतरित कोण ज्ञात कीजिए।
सिद्ध कीजिए कि एक त्रिभुज के किसी कोण का समद्विभाजक और उसकी सम्मुख भुजा का लंब समद्विभाजक, यदि प्रतिच्छेद करते हैं तो, उस त्रिभुज के परिवृत्त पर प्रतिच्छेद करते हैं।
AB और AC त्रिज्या r वाले एक वृत्त की दो जीवाएँ इस प्रकार हैं कि AB = 2AC है। यदि p और q क्रमश : केंद्र से AB और AC की दूरियाँ हैं, तो सिद्ध कीजिए कि 4q2 = p2 + 3r2 है।
निम्नलिखित आकृति में, O वृत्त का केंद्र है और ∠BCO = 30° है। x और y ज्ञात कीजिए।
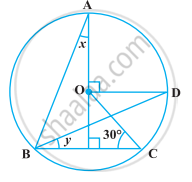
निम्नलिखित आकृति में, O वृत्त का केंद्र है, BD = OD और CD ⊥ AB है। ∠CAB ज्ञात कीजिए।