Advertisements
Advertisements
प्रश्न
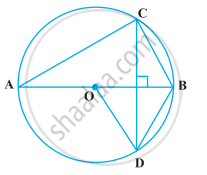
निम्नलिखित आकृति में, O वृत्त का केंद्र है, BD = OD और CD ⊥ AB है। ∠CAB ज्ञात कीजिए।
उत्तर
दिया गया है, आकृति में BD = OD, CD ⊥ AB।
∆OBD में, BD = OD ...[दिया गया है।]
OD = OB ...[दोनों वृत्त की त्रिज्या हैं।]
∴ OB = OD = BD
इस प्रकार, ∆OBD एक समबाहु त्रिभुज है।
∴ ∠BOD = ∠OBD = ∠ODB = 60°
ΔMBC और ΔMBD में,
MB = MB ...[उभयनिष्ठ पक्ष]
∠CMB = ∠BMD = 90°
और CM = MD ...[एक वृत्त में जीवा पर डाला गया कोई लंब जीवा को समद्विभाजित करता है ।]
∴ ΔMBC ≅ ΔMBD ...[SAS सर्वांगसमता नियम द्वारा]
∴ ∠MBC = ∠MBD ...[CPCT द्वारा]
⇒ ∠MBC = ∠OBD = 60° ...[∵ ∠OBD = 60°]
चूँकि, AB वृत्त का व्यास है।
∴ ∠ACB = 90°
∠ACB में, ∠CAB + ∠CBA + ∠ACB = 180° ...[त्रिभुज के कोण योग गुण द्वारा]
⇒ ∠CAB + 60° + 90° = 180°
⇒ ∠CAB = 180° – (60° + 90°) = 30°
APPEARS IN
संबंधित प्रश्न
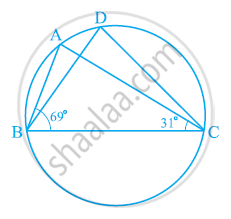
आकृति में, ∠ABC = 69° और ∠ACB = 31° हो, तो ∠BDC ज्ञात कीजिए।
निम्नलिखित आकृति में, यदि AOB एक व्यास है और ∠ADC = 120° है, तो ∠CAB = 30° है।
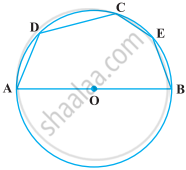
AB और AC एक वृत्त की दो बराबर जीवाएँ हैं। सिद्ध कीजिए कि ∠BAC का समद्विभाजक वृत्त के केंद्र से होकर जाता है।
किसी वृत्त की एक जीवा उसकी त्रिज्या के बराबर है। इस जीवा द्वारा दीर्घ वृत्तखंड में किसी बिंदु पर अंतरित कोण ज्ञात कीजिए।
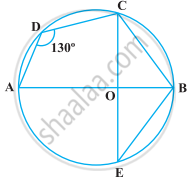
निम्नलिखित आकृति में, ∠ADC = 130° और जीवा BC = जीवा BE है। ∠CBE ज्ञात कीजिए।
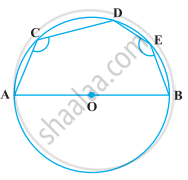
निम्नलिखित आकृति में, AOB वृत्त का व्यास है तथा C, D और E अर्धवृत्त पर स्थित कोई तीन बिंदु हैं। ∠ACD + ∠BED का मान ज्ञात कीजिए।
सिद्ध कीजिए कि एक त्रिभुज के किसी कोण का समद्विभाजक और उसकी सम्मुख भुजा का लंब समद्विभाजक, यदि प्रतिच्छेद करते हैं तो, उस त्रिभुज के परिवृत्त पर प्रतिच्छेद करते हैं।
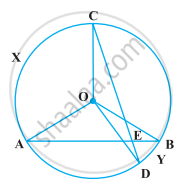
निम्नलिखित आकृति में, AB और CD एक वृत्त की दो जीवाएँ हैं, जो E पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि AEC = `1/2` (चाप CXA द्वारा केंद्र पर अंतरित कोण + चाप DYB द्वारा केंद्र पर अंतरित कोण) है।
AB और AC त्रिज्या r वाले एक वृत्त की दो जीवाएँ इस प्रकार हैं कि AB = 2AC है। यदि p और q क्रमश : केंद्र से AB और AC की दूरियाँ हैं, तो सिद्ध कीजिए कि 4q2 = p2 + 3r2 है।
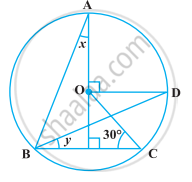
निम्नलिखित आकृति में, O वृत्त का केंद्र है और ∠BCO = 30° है। x और y ज्ञात कीजिए।