Advertisements
Advertisements
प्रश्न
केंद्रों O और O' वाले दो वृत्त बिंदुओं A और B पर प्रतिच्छेद करते हैं। A (या B) से होकर एक रेखा PQ रेखाखंड OO' के समांतर खींची जाती है, जो वृत्तों को P और Q पर प्रतिच्छेद करती है। सिद्ध कीजिए कि PQ = 2 OO' है।
उत्तर
सबसे पहले O और O' को केंद्र लेकर दो वृत्त इस प्रकार बनाएं कि वे A और B पर प्रतिच्छेद करें।
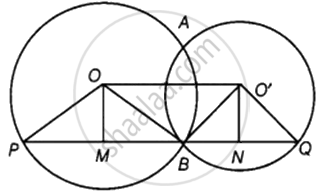
OO' के समानांतर एक रेखा PQ खींचिए।
केंद्र O वाले वृत्त में, हमारे पास है -
OP और OB वृत्त की त्रिज्याएँ हैं।
PB जीवा है, जिसका लम्ब समद्विभाजक OM है।
यानी BM = MP ...(1)
केंद्र O' वाले वृत्त में, हमारे पास -
O'B और O'Q वृत्त की त्रिज्याएँ हैं।
BQ जीवा है और O'N इसका लम्ब समद्विभाजक है।
यानी BN = BQ ...(2)
(1) और (2) से, हमारे पास -
BM + BN = MP + NQ
⇒ (BM + BN) + (BM + BN) = (BM + BN) + (MP + NQ)
⇒ 2(BM + BN) = (BM + BN) + (MP + NQ)
⇒ 2(OO') = (BM + MP) + (BN + NQ)
⇒ 2(OO') = BP + BQ
⇒ 2(OO') = PQ
अत: सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
याद कीजिए कि दो वृत्त सर्वांगसम होते हैं, यदि उनकी त्रिज्याएँ बराबर हों। सिद्ध कीजिए कि सर्वांगसम वृत्तों की बराबर जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करती हैं।
सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों की जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करें, तो जीवाएँ बराबर होती हैं।
यदि BM और CN त्रिभुज ABC की भुजाओं AC और AB पर खींचे गए लंब हैं, तो सिद्ध कीजिए कि बिंदु B, C, M और N चक्रीय हैं।
यदि P, Q और R क्रमश : एक त्रिभुज की BC, CA और AB भुजाओं के मध्य-बिंदु हैं तथा AD शीर्ष A से BC पर लंब है, तो सिद्ध कीजिए कि बिंदु P, Q, R और D चक्रीय है।
यदि एक चक्रीय चतुर्भुज ABCD के सम्मुख कोणों के समद्विभाजक इस चतुर्भुज के परिगत वृत्त को P और Q, बिंदुओं पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि PQ इस वृत्त का व्यास है।
